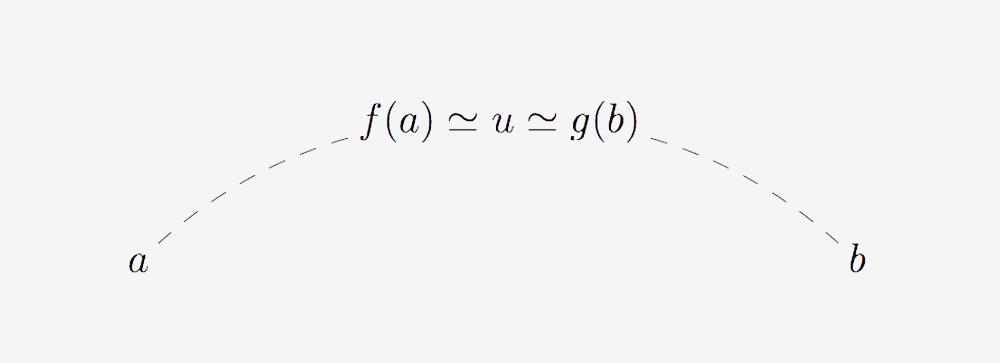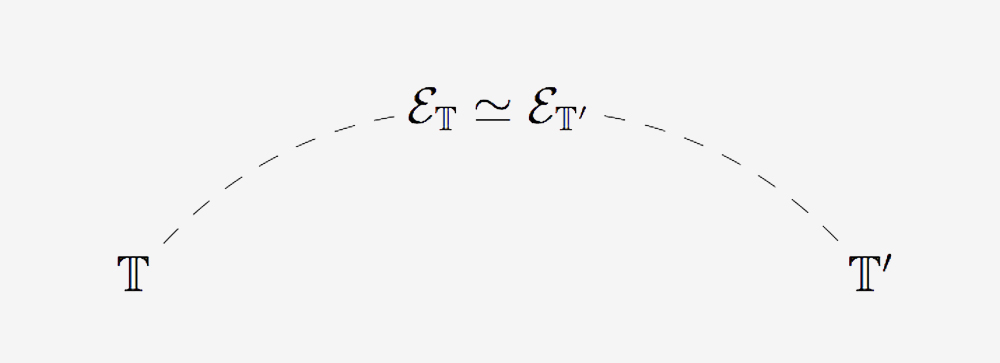Mathematics is divided into several distinct areas: geometry, number theory, algebra, analysis, mathematical logic, etc. Each of these areas has evolved throughout the years by developing its own ideas and techniques, and by now has reached a remarkable degree of specialization. Now, even more than in the past, we feel the need for unifying theories that could intra-disciplinarily connect different areas of mathematics with their different sets of concepts, objects, and methods, in new and powerful ways, hence providing effective tools for solving long-standing problems. It has happened several times that solutions to profound problems in one field have first, or only, been obtained by using methods from other fields, and this indicates that Mathematics should be seen as a coherent whole rather than a collection of separate fields. Think for example of analytic geometry, which allows the study of geometrical shapes using algebraic manipulation, or the Grothendieckian notion of spectra, which allows the study of discrete objects using a geometric continuous intuition.
The importance of ‘bridges’ between different areas lies in the fact that they make it possible to transfer knowledge and methods between the areas, so that problems formulated in the language of one field can be tackled (and possibly solved) using techniques from a different field, and results in one area can be appropriately transferred to results in another.
A few years ago, I had the intuition that the theory of Grothendieck toposes could provide a powerful means for unifying different mathematical theories. More precisely, I imagined that the possibility of representing toposes in multiple ways could be exploited for building ‘bridges’ interconnecting different theories and allowing a transfer of information between them.
Toposes are abstract logical concepts that lie at a level of generality which is ideal for shedding light on Mathematics as a whole. To any mathematical theory of a very general form (pertaining to algebra, geometry, or any other mathematical field) one can associate a topos, called the classifying topos of the theory, which embodies its essential features (i.e., precisely those features which are invariant under a general notion of equivalence of theories). This enables us to study theories by studying their classifying toposes. Different theories may be classified by the same topos; this means precisely that they describe the same structures in different languages. The existence of different theories classified by the same topos translates, at the technical level, into the existence of multiple representations for that topos. The latter can then be used as a ‘bridge’ for transferring properties, notions and results across those theories.
Throughout the past years, I have developed a set of interdisciplinary methods and techniques for effectively using toposes as unifying ‘bridges,’ and, in doing this, I have uncovered a number of connections between different mathematical theories that were previously hidden and, in many cases, even unsuspected. This intuition has been supported first by some initial results and then comforted these past years by new evidence, some of which provided the solution to long-standing problems. By now a substantial body of mathematical results has been produced: this includes a number of deep applications into distinct fields such as Algebra, Geometry, Topology, Functional Analysis, Model Theory, and Proof Theory.
The purpose of this article is to give a conceptual introduction, accessible to non-specialists, to the theory of topos-theoretic ‘bridges.’1 The last section of the paper is more technical and requires a basic familiarity with logic and category theory to be properly understood.2
The Concept of Unification
Before we proceed any further, let us first clarify the meaning of the term ‘unification,’ as it is somewhat ambiguous and can be used with different significations.
‘Static’ and ‘Dynamic’ Unification
We can distinguish two different kinds of unification: ‘static’ and ‘dynamic.’
. With ‘static’ unification (through generalization), two concepts are seen to be special instances of a more general concept:
Results that apply to the general concept may be specialized to yield results on the two more particular concepts.
. With ‘dynamic’ unification (through construction), on the other hand, two objects are related to each other through a third one (usually constructed from each of them), which acts as a ‘bridge’ enabling the transfer of information between them:
The transfer of information arises from the process of ‘translating’ properties (or constructions) on the ‘bridge object’ into properties (or constructions) on the two objects.
We call the first form of unification ‘static’ in light of the fact that recognizing two different concepts as particular cases of a more general one does not in and of itself offer a way for transferring information between them. For example, the fact that both preorders and groups are particular instances of the general notion of category does not by itself provide a means of transferring results about preorders to results about groups, or vice versa.
On the other hand, the second form of unification allows a ‘dynamic’ transfer of information between the two given objects. Indeed, the third object which is associated or constructed from each of the two objects admits two different ‘representations,’ corresponding to the two different ways of constructing it from each of the two objects. Such an object thus yields ‘bridges’ between the two given objects in the sense that information can be transferred between them by translating properties of (or constructions on) the bridge object into properties of (or constructions on) the two objects, by exploiting its two different representations.
Let us illustrate the difference between these two kinds of unification using some notable mathematical examples.
By providing a system in which all the usual mathematical concepts can be expressed rigorously, Set Theory represented the first serious attempt of Logic to unify Mathematics, at least at the level of language. Later, Category Theory provided an alternative abstract language in which most of Mathematics can be formulated and, as such, has represented a further advancement towards the goal of ‘unifying Mathematics.’ Anyway, both of these systems realize a ‘static’ unification in that, whilst each of them provides a way of expressing and organizing Mathematics in one single language, they do not by themselves offer effective methods for an actual transfer of knowledge between distinct fields.
On the other hand, the theory of topos-theoretic ‘bridges’ provides a systematic way to compare distinct mathematical theories with each other and to transfer knowledge between them. In this setting, the two objects to be related to each other are distinct mathematical theories which share a common ‘semantic core,’ while the bridge object is a Grothendieck topos representing precisely this common ‘core.’
As a given ‘bridge object’ can in general interconnect not just two objects but many different pairs of objects, so in the topos-theoretic setting, for each topos there exist infinitely many different mathematical theories associated with it (through the classifying topos construction).
Other instances of dynamic unification certainly occur in Mathematics; in fact, invariants are always sources of ‘bridges’ between objects on which they are defined. So, for example, the fundamental group of a topological space can be used as a bridge for transferring information between topological spaces, in the sense that if two topological spaces have isomorphic fundamental groups, then certain topological properties, such as simple connectedness, can be transferred across the spaces. Similarly, groups can be used to classify geometries, as in Klein’s Erlangen Program, etc.
The startling aspect of toposes is that, unlike most of the invariants considered in Mathematics, they allow us to compare and effectively interconnect mathematical theories that may belong to several different subfields of Mathematics.
The Idea of ‘Bridge’
One is generally interested in comparing pairs of objects between which there is some kind of relationship.
In order to transfer information between objects related by a given relationship, it is thus of fundamental importance to identify (and, possibly, classify) the properties of the objects that are invariant with respect to that relationship.
Depending on the cases, this can be a reasonably manageable task or a hopelessly difficult one. In fact, a relationship between two given objects is generally an abstract entity, which lives in an ideal context that is normally different from that in which the two objects lie.
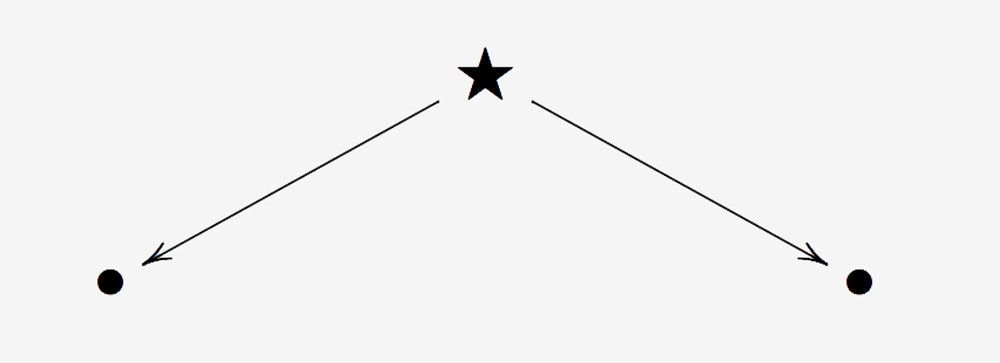
It thus becomes of crucial importance to identify more concrete entities that could act as ‘bridges’ connecting the two given objects. We can think of a bridge object connecting two objects a and b as an object u which can be ‘built’ from any of the two objects a and b, and which admits two different representations f(a) and g(b) related by some kind of equivalence ≃, the former representation being in terms of the object a and the latter in terms of the object b:
The transfers of information arise from the process of ‘translating’ ≃- invariant properties of (or constructions on) the ‘bridge object’ u into properties of (or constructions on) the two objects a and b by using the two different representations of u. Notice that the invariance with respect to ≃ is essential in order to be able to regard the given property of (or construction on) u both from the point of view of a, by using f, and from the point of view of b, by using g. Of course, such a ‘bridge’ is more or less useful depending on whether the ‘encodings’ f and g are sufficiently well-behaved to allow genuine ‘unravellings’ of the given property of (or construction on) f(a) (respectively of g[b]) in terms of properties of (or constructions on) a (respectively of b).
The idea of ‘bridge’ is strictly related to that of ‘invariant construction.’ Given two sets I and O, and two equivalence relations ≃I and ≃O respectively on I and on O, we may define an invariant construction f: (I,≃I) → (O,≃O) as a function f: I → O which respects the equivalence relations (i.e., such that whenever x ≃I y, f(x) ≃O f(y)). We say that f is conservative if it reflects the equivalence relations (i.e., whenever f(x) ≃O f(y), x ≃I y). Given an invariant construction f: (I, ≃I) → (O, ≃O), a bridge object connecting two objects x, y ∈ I is an object b ∈ O such that b ≃O f(x) and b ≃O f(y). Given a conservative invariant construction f: (I, ≃I) → (O, ≃O), bridge objects in O, considered up to ≃O-equivalence, can be thought of as classifying objects, since they can be taken as canonical representatives of ≃I-equivalence classes.
Of course, a ‘bridge’ of this kind is most useful in classifying ≃I -invariant properties in cases in which it is more manageable to work with objects of type O than with objects of type I, or when the relation ≃O is more tractable than the relation ≃I.
As we shall see below, in the context of the theory of topos-theoretic ‘bridges’ the objects to be compared with each other are mathematical theories (formalized within a kind of first-order logic), while the invariant construction is given by the classifying topos construction.
Structural Translations
The bridge method can be interpreted linguistically as a methodology for translating concepts from one context to another. But which kind of translation is this? Generally speaking, we distinguish between two essentially different approaches to translation:
1) the ‘dictionary-oriented’ or ‘bottom-up’ approach, consisting in a dictionary-based renaming of the single words composing the sentences, and
2) the ‘invariant-oriented’ or ‘top-down’ approach, consisting in the identification of appropriate concepts that should remain invariant in the translation, and in the subsequent analysis of how these invariants can be expressed in the two languages.
As would be expected, translations of the former kind, though occasionally useful, are not intrinsically profound in that they do not change the ‘shape’ of the sentences on which they operate and hence do not provide significantly different ways for conveying a certain message. On the other hand, the invariant-oriented translations are liable to significantly change the syntactical form used to express a certain meaning, and thus to generate new insights and points of view on the given message. We shall come back to this topic below.
Translations across distinct mathematical theories realized through bi-interpretations between them are of the former kind. Indeed, bi-interpretation acts as a sort of dictionary for translating formulae written in the language of the first theory into formulae written in the language of the second. On the other hand, ‘bridge-based’ translations, and in particular topos-theoretic ones, are of the latter kind. In fact, in the context of the theory of topos-theoretic ‘bridges,’ the invariant properties are topos-theoretic invariants defined on toposes, and the expression of these invariants in terms of the two different theories is essentially determined by the structural relationship between the topos and its two different representations.
Some Examples of ‘Bridges’ in Science
In order to illustrate the concept of the ‘bridge’ as explained above, let us discuss a few scientific situations that can be naturally interpreted in terms of ‘bridges.’
Astronomy: The ‘Classifying Star’ of a Planet
The universe is composed of several stars, around which revolve certain bodies, called planets. Different planets can revolve around a given star, but every planet revolves around a single star, which we call the planet’s classifying star.
The trajectory that a given planet makes around its classifying star is determined by two sets of ingredients, namely the parameters determining the ellipse and the period of revolution around its classifying star. This pair (ellipse parameters and period of revolution) for a given planet determines its orbit and its classifying star. The classifying star can be identified uniquely from any planet that is classified by it (equivalently, from the pair associated with it), and represents the ‘right’ point of view from which one should observe it (in fact, the elliptic motion of a planet looks very weird if observed from any other point of view than one of its foci).
Different planets revolving around the same star can be studied in relation to each other using properties of the common classifying star, which therefore acts as a ‘bridge object’ across them. In fact, there are natural relationships between properties of planets and properties of the stars around which they revolve.
To have an idea of the use of ‘bridges’ in Astronomy, think for example of Kepler’s laws. The property that all the planets revolving around a given star have elliptic orbits can be regarded as an invariant property of stars (or, more generally, of bodies around which other bodies revolve). The concrete orbit of a given planet can be seen as arising from the process of expressing this abstract invariant ‘the orbits are elliptic’ in terms of the concrete pair associated with the given planet. So the forms of the orbits of two distinct planets around the same star represent different instances of a unique abstract pattern.
Also, it is often the case that by investigating the features of a given planet, one can infer properties of its classifying star, and that these properties can in turn be ‘reflected back’ into properties of another planet revolving around the same star. For example, the third Kepler’s law asserts that the ratio of the square of the orbital period of a planet by the cube of the semi-major axis of its orbit is a constant that is characteristic of the star and does not depend on the given planet. This principle can thus be regarded as an invariant property of stars (or, more generally, of bodies around which other bodies revolve), and the concrete trajectories made by the planets can be interpreted as different manifestations of this abstract property in the context of the distinct (pairs associated with the) planets. The common classifying star can thus be used as a ‘bridge’ to transfer information between the two planets; indeed, the investigation of the concrete trajectory of a planet can allow one to infer the characteristic constant of its classifying star, and this piece of information in turn constrains the concrete trajectory of any other planet revolving around it.
Linguistics: ‘Bridges’ for Translating
A fundamental feature of a translation is the set of abstract properties of texts (for example, the ‘meaning,’ the ‘musicality,’ ‘structural’ characteristics, etc.) which it leaves invariant.
A literal translation proceeds in a bottom-up or dictionary-oriented way, as it consists, broadly speaking, in splitting the given text into sentences and then into words or short expressions, replacing each word (or short expression) in the first language with a word (or short expression) in the other language that corresponds to it according to a given dictionary, and then assembling these words together ‘from the bottom up,’ following the same or at most a similar grammatical structure to that in which the corresponding words (or short expressions) were arranged in the original text. From this description, it is clear that what is preserved by this kind of translation is the syntactical structure of the sentences that make up the texts, but not necessarily the meaning or musicality of the texts, which is what one would naturally expect from a good translation. This is why automatic or literal translations are not always possible, and even when they are, are often rather unsatisfactory, especially when they occur between languages that have radically different syntactical ways of expressing a given meaning.
This naturally raises the following question: what type of approach should one adopt to obtain a good translation? Unlike a literal translation, a good translation should proceed in a top-down or invariant-oriented way, starting with the identification of a set of abstract properties of texts that one would like to preserve in the translation, and then using any such property P (or the ‘intersection’ of all such properties) as a ‘bridge’ for translating between the two languages, as follows. For each such P one looks at the way P is best expressed in the first language, and then at the way P can be best conveyed in the second language; the resulting expressions are then set to correspond to each other in the translation.
Note that in a translation of this kind, it is not necessarily the syntactical structure that must be preserved, as in the case of a literal translation, but rather the properties defined at the beginning as the chosen invariants. While a literal translation is neither particularly interesting nor conceptually profound, in that it essentially consists in a re-naming or re-labeling of the primitive constituents of a text according to a dictionary, a good literary translation is often a work of art which may reveal new aspects of a text that were, in a sense, ‘hidden’ in the original version, allowing new and different interpretations of the message.
Genetics: the DNA as a ‘Bridge’
(Human) DNA embodies many of the essential features of the individual to which it belongs, but is invariant with respect to contingent features of the individual, such as its particular physical appearance at a given time (or its age).
The DNA is essentially unique to each individual but it can be extracted from him/her in many different ways (for example, from different parts of the body). Many specific features of individuals are reflected in particular features of their DNA.
This makes the DNA a particularly suitable object for acting as a ‘bridge’ for transferring information across different individuals. For instance, the discovery of similarities between the DNA of different individuals may reveal parental relationships between them or similar predispositions to certain diseases.
Notice that the kind of insight that the investigation of DNA can provide cannot be obtained with alternative methods: indeed, only by using this level of analysis can one unveil the ‘hidden’ features of individuals encoded within the DNA.
This is similar to what happens in Topos Theory: the notion of a classifying topos of a theory plays the role of a sort of DNA of the theory, the investigation of which can reveal aspects of the theory that are barely visible with other techniques. As in Genetics one studies how modifications of the DNA influence the characteristics of an individual, so in Topos Theory one can study the effect that topos-theoretic operations on toposes have on the theories classified by them.
Ideal = Real?
Bridges abound both in Mathematics and in other scientific fields, and can be considered ‘responsible’ (at least abstractly) for the ‘genesis’ of things and the nature of reality as we perceive it. The idea of bridge is an abstraction, but, interestingly, bridges arising in the experimental sciences can often be identified with actual physical objects. In fact, the most enlightening situations occur when these ideal objects admit concrete representations, allowing us to contemplate the dynamics of ‘differentiation from the unity’ in all its aspects.
Grothendieck toposes allow us to materialize a tremendous number of ideal objects, and hence to establish effective bridges between a great variety of different contexts. In general, looking for ‘concrete’ representations of ‘imaginary concepts’ can lead to the discovery of more ‘symmetric’ environments in which phenomena can be described in natural and unified ways.
Toposes as ‘Bridges’
Now that we have extracted the essential conceptual features of the ‘bridge’ technique, we can proceed to illustrating its implementation in the context of topos theory.
The General Methodology
The theory of topos-theoretic ‘bridges’ is centered around the concept of Grothendieck topos.3 The theory of Grothendieck topos is written in categorical language, but, unlike Category Theory, it is much more expressive, due to an additional degree of freedom implicit in the definition of topos. Indeed, a category can be thought of as a pair of sets related by some structure satisfying certain properties; any set can be regarded as a category, but most of the categories arising in Mathematics are not of this form. In fact, the concept of category has, with respect to the notion of set, an additional degree of freedom.
Toposes are mathematical objects which are built from a pair, called a site, consisting of a category C and a generalized notion of covering J on it in a certain canonical way (called Grothendieck topology). The process that produces a topos from a given site can be described as a sort of ‘completion’ with respect to certain categorical operations relative to which the category C might not be closed. Formally, a topos is defined as a category Sh(C, J) of sheaves on a site (C, J).
Different coverings can be considered on a given category, generally leading to inequivalent toposes; this gives the notion of topos one more degree of freedom with respect to that of category. The existence of these three ‘degrees of freedom’ implicit in the concept of a topos (two for the notion of category and one for that of Grothendieck topology) can be exploited to build ‘mathematical universes’ in which mathematical theories find their natural home and can be effectively compared with each other.
In fact, thanks to the pioneering work of Makkai and Reyes in the seventies,4 to any mathematical theory (of a general specified form, technically speaking a geometric theory) one can canonically associate a topos called the classifying topos of T, which represents the natural framework in which the theory should be investigated, both in itself and in relationship to other theories. Two theories having the same classifying toposes (up to equivalence) are said to be Morita-equivalent.
The existence of theories that are Morita-equivalent to each other translates, at the level of sites, into the existence of different sites generating the same topos (up to equivalence); indeed, to any theory one can canonically associate a site such that the topos built from it can be identified with its classifying topos.
The classifying topos of a theory can be effectively used as a ‘bridge’ to transfer information between the theory and any other theory that is Morita-equivalent to it, as follows. For any given property or construction of toposes which is invariant under equivalence of toposes (one requires this invariance because the classifying topos is determined only up to equivalence), one tries to express it first in terms of one theory and then in terms of the other; provided that one obtains appropriate characterizations connecting properties of theories and properties of their classifying toposes (equivalently, characterizations connecting properties of sites and properties of toposes). This will lead to a logical relationship between properties of the two theories written in their respective languages:
Technically, the transfer of information across the two theories is realized by attaching to the two theories suitable sites of definition for their classifying topos (or objects of a different kind representing their classifying topos), and expressing topos-theoretic invariants on the given classifying topos in terms of these two sites by means of ‘site characterizations’:
A striking aspect of this technique, in addition to its level of generality (indeed, it can be applied to mathematical theories belonging essentially to any mathematical field), is the fact that it can be automated in many cases. Indeed, using the methods of Topos Theory one can obtain characterizations of the above kind for several invariants, holding uniformly for any theory or at least for wide classes of theories (and for certain classes of invariants such characterizations can even be established in a purely mechanical way); in the presence of a Morita-equivalence, these characterizations will thus be able to act as the ‘arches’ of a ‘bridge’ connecting the two theories, making it possible to transfer information between them.
As is naturally expected, the translations between properties of Morita-equivalent theories realized by means of the ‘bridge’ technique can be very surprising. Indeed, a unique abstract invariant property defined at the topos-theoretic level may be expressed in completely different ways in terms of different sites of definition of a given topos.
As an example, consider the property of completeness of a theory: a geometric theory is said to be complete if every geometric assertion written over its language is either provably true or provably false in the theory. Proving that a theory is complete is generally a difficult matter. Nonetheless, this property is equivalent to a simple invariant property of the classifying topos (namely, its property of being two-valued), admitting alternative reformulations in terms of other sites of definition.
For instance,5 this invariant property is equivalent to the joint embedding property on a category C (i.e., the property that any two objects in the category can be mapped to a third one) in the case of a non-trivial atomic site (Cop, Jat) (keeping in mind that the atomic topology Jat on the dual of a category C satisfying the amalgamation property is the Grothendieck topology having as covering sieves precisely the non-empty ones). Notice that the joint embedding property on a category is generally a much simpler way to verify a property than the completeness of a theory; nonetheless, for theories T whose classifying topos is a topos of sheaves on an atomic site (Cop, Jat), the two properties (i.e., completeness of T and joint embedding property of C) correspond to each other under a topos-theoretic ‘bridge,’ which thus allows one to be established by verifying the other.6
Why Toposes?
One might wonder what makes Grothendieck toposes so effective in serving as ‘bridges’ for connecting different mathematical theories with each other. There are several reasons for this, which we can summarize as follows:
. Generality: Unlike most of the invariants used in Mathematics, the level of generality of topos-theoretic invariants is such that they are suitable for comparing (first-order) mathematical theories of essentially any kind.
. Expressivity: Many important invariants arising in Mathematics can be expressed as topos-theoretic invariants.
. Centrality: The fact that topos-theoretic invariants often specialize to important properties or constructions of natural mathematical or logical interest is a clear indication of the centrality of these concepts in Mathematics. In fact, whatever happens at the level of toposes has ‘uniform’ ramifications in Mathematics as a whole.
. Technical flexibility: Toposes are mathematical universes that are very rich in terms of internal structure; moreover, they have a very well-behaved representation theory, which makes them extremely effective computationally when considered as ‘bridges.’