According to Pierre Francastel, “Art and mathematics are the two poles of any logic thinking—the major thinking modes of humanity.”1 In fact, since Greek Antiquity, art and mathematics have always nurtured a natural dialogue, forming together a tissue of opposed polarities, fruitful tensions and partial osmoses. Concepts, symbols and materials often separate the artist and the mathematician, but a common strategy—to think and imagine through dialectic, relational webs—brings them together. For Francastel, “As the mathematician … combines schemes of representation and prediction where the real is associated with the imaginary, so the artist confronts elements of representation with other imagination issues. In both cases, the dynamism of a thought that becomes aware of itself by expressing itself and materializing itself in ‘signes-relais’ [“relay-signs”] extends and encompasses elements of experience and those of the logic of the mind.”2 The transits between reality and imagination, the Many and the One, the particular and the universal, the local and the global, constitute the very core of mathematical and artistic creativity. If their signes-relais are often different (and, in some cases, the specificity of mathematical signes-relais preclude the possibilities the artist has of entering into the realm of mathematics), the underlying relational protogeometry which governs the intertwining of the different signs can be extremely close.
In what follows, fragments of that common relational protogeometry will be revealed, and will be applied to an understanding of some strong weaving dynamics in contemporary art and mathematics. Referring to The Glass Bead Game, Hesse mentions in a 1943 letter how his game and Castalia were meant “not as eternally valid ideals, but as potential worlds, conscious of their own relativity.”3 Relationality, potentiality, and relativity, are in fact key twentieth-century forces. Contrary to popular interpretation, entanglement and intersection, built over a non-absolute ground, do not necessarily lead to postmodern skepticism. As Knecht writes at the end of his Waldzell encounter with Designori, “The entire life, whether physical or spiritual, is a dynamic phenomenon, of which the Glass Bead Game contemplates its esthetic side, especially through the framework of rhythmic phenomena.”4 Following Castalia’s Magister Ludi, the mesh of materiality and spirituality, the crossings and echoes along reason and imagination, the intertwined rhythmic spectrum of all senses, the dynamic blend of polarities, are not only still possible, but become really potentiated in our transmodern world, as Glass Bead‘s research platform and journal are demonstrating.

Drawing by Charles Sanders Peirce (The Peirce Papers, Harvard University)
The roots of a unified, non-foundational vision that encompasses art and mathematics as fragments of a multidimensional protogeometry of culture can be traced back at least to Novalis (end of the eighteenth century). Riemann surfaces (mid-nineteenth century) partially solve the tensions and ramifications between the Many and the One, in the mathematical domain of complex variables. Peirce’s pragmaticism (end of the nineteenth century) offers a general architectonics of knowledge, where phenomenological obstructions and transits help to explain the emergence of creativity. If we consider fragments and ramifications as residues, or strata, and we focus our vision on the history of art, Warburg’s Mnemosyne Atlas (early twentieth century) provides another main reference to unveil the complex protogeometry of cultural exchanges. Profiting from dual definitions of art and mathematics proposed by Focillon and Lautman (mid-twentieth century), we can then set up a faithful panorama of the strong dialectics in play. Finally, through the invention of mathematical category theory and its developments in the work of Grothendieck and followers (end of the twentieth century), deep non-classical logics and non-separated geometries (sites and sheaves in Grothendieck toposes) can be used to further clarify the oppositions and conciliations between art and mathematics.
The first section of this paper presents diverse forms of dialectics between art and mathematics, following Novalis, Warburg, Focillon and Lautman. The second section explores some tensions between the local and the global, both in art and mathematics, profiting from Peirce’s architectonics. The third and final section proposes embedding the local/global dialectics in art and mathematics along multilayered surfaces (coming from Riemann surfaces) and multidimensional sites (coming from Grothendieck toposes), governed by continuous, intuitionistic logics.
1.Dialectics between Art and Mathematics
Due to the unavoidable opacity of mathematical signes-relais, mathematical creativity is seldom understood outside its practitioners. Nevertheless, a sustained French tradition has delved into the question,5 revealing the complex weaving of inventiveness in mathematics. From the concrete (multitude of careful examples) to the abstract (general representation patterns), from a precise reckoning of difference (existence and uniqueness theorems in local frames) to all-encompassing integral views (universal structures and mathematical categories), from syntactical restraint (proof theory) to semantic freedom (model theory), from full control (deduction, rational clearness) to glimpses of error (abduction, imaginative mess), mathematics breaks all supposedly rigid forms of knowledge. Plasticity then becomes one of the essential characteristics of mathematical thought (see Section 2, for an understanding of conceptual mathematical elasticity—iteration and deiteration—using Peirce’s three cenopythagorean categories).
On another hand, Novalis had admonished that, while science required plasticity, poetry required exactitude. In fact, beyond usual prejudices, artistic creativity has been built on extreme accuracy. Imaginal invention synthesizes, in unique images, sophisticated webs of correlations of the image with its surroundings, either material or conceptual. As sorts of residues (which recall Benjamin’s search for remainders in his Paris Arcades project), the images reflect and potentiate the contexts where they are introduced. An emergence of sense comes often from the surprise effect of accurately distorted, limiting images. Artistic signes-relais profit from a forceful materiality that can embed polysemy and multiverse problems in the very rawness of matter. In this way, mathematics and art produce a first dialectics (A), tensioning the field of knowledge in opposite, complementary ways (like the polarities in an electromagnetic field): revealing and universalizing in mathematics, blurring and particularizing in art. What becomes essential is that, in middle grounds, both art and mathematics converge: the great, singular artistic chef d’oeuvre opening up unexpected universal dimensions, and the great, universal mathematical chef d’oeuvre projecting itself in equally unexpected, singular models.
In La vie des formes (1934), Focillon suggested a definition of art as the space where “la forme se signifie”6 (“form signifies itself”). Thus, art deals with forms which have to be structured, in order to obtain their significance. Inversely, following a dual approach, we may think of a definition of mathematics as the space where “la signification se forme” (“signification forms itself”). Even if that quote does not appear explicitly in Lautman’s Thèses (1937), all his work7 explains how mathematics deals with structures which have to be formed, in order to obtain their theorematic force. A natural, second dialectics (B) between art and mathematics emerges through these dual definitions. In this way, an understanding of the fabric of tensions between form and structure grows to be one of the central problems to be studied in the interrelationships between art and mathematics. As we will see in Section 2, dialectics (B) can be iterated along several levels—according to Peirce’s phenomenological categories and according to transfers along mathematical category theory—which can be explored through multilayered geometries and multivalued logics.
Novalis had already urged that a superior dialectics has to take into account serious antinomies, and, even beyond clashes of two polarities, has to understand infinitomies: Beyond duality, and trivial separation, “science does not begin by an antinomy—or a binomial—rather by an infinitomial.“8 The young genius underlines the importance of an “inversion of the three logical principles—from which are derived the three logical antinomies and the three fundamental problems”9 (the three principles, according to Leibniz, are the principles of identity, non-contradiction, and sufficient reason). In particular, the problem of understanding the contradiction p∧¬p (inverting the principle of non-contradiction, and accepting antinomies) fosters some of the more original insights of the poet. Building on several potentialities of antinomic thinking—”antinomy of intention, project and process … antinomy of concept and object … antinomy of proof and solution …”10 —Novalis introduces a powerful relative geometry, where “time and space are ever interchanging,” where “the law of the excluded middle does not apply,” and where diverse worlds (interior/exterior, mind/nature, culture/science) are “admixed,” forming “part of a continuum.”11
Mathematics and art do form part of that continuum. For Novalis, “creative imagination” is tri-composed of reason, judgment and sensibility.12 Breaking artificial frontiers, going beyond simple partitions and compartments, art and mathematics enter a perpetuum mobile space, to be examined through a sophisticated topology of transits. A third dialectics (C) between art and mathematics faces then the problem of rendering continuous the (apparently) discrete oppositions. In his Mathematical studies on Murhard (c. 1798), Novalis writes: “In all sciences one has spontaneously to plasticize [plastisirt].”13 Transitions, translations, transferences, transformations, transfigurations, are repeated terms in Novalis’ writings. The trans/ concept plasticizes all his thinking. Mathematics and art participate strongly in that trans/ philosophy, which, as many cultural movements of the new millennium are showing, is becoming a basic concern of our times. Some alternative journals, open to non-separated thought, where art, science and philosophy are well “admixed”—such as Collapse, one of the most brilliant adventures of thought produced in the last ten years, and Glass Bead, hopefully a brilliant companion in the near future—reflect that trans/ imperative.
Warburg’s Mnemosyne Atlas (1924-1929) investigates the transformation of images in Western thought and their roots in the Near East. The Atlas looks to provide an orientation of man’s actions inside the weft of culture, and, as the Mnemosyne mythological echo suggests, it tries to (re)construct a site thanks to an exploration of the remainders of memory. For Warburg, the very foundation of the project lies in a precise, creative antinomy: “Image and number as an anti-chaotic polar function of memory serving orientation.”14 Thus, the very polarity of art (images) and mathematics (numbers) is set to organize, in an explicitly non-chaotic way, all types of strata, ruins, residues, traces, proper of historical researches (for a long study on Warburg’s connection between antinomic and creative thinking).15 The Introduction to the Atlas Mnemosyne unfolds a dozen terms related to “polarité” and “opposition.”16 “The bounding poles of psychic behavior: calm contemplation on the one hand, and orgic fervor on the other”17 also represent the limiting “regions” of mathematics and art. Along a dynamical system, reason and sensibility (or Creation and Life, as in Death in Venice [1912]) produce a fourth dialectics (D) between mathematics and art, where the principal issue becomes to situate local residues inside global webs, and to understand their new harmonics (or, better, their non-harmonics, either creative18 or theoretical).19
2.Local/Global Transits in Art and Mathematics: A Peircean Approach
When faced with contemporary art and mathematics, we cannot escape a certain transitory ontology,20 that—at first, terminologically speaking—seems self-contradictory. Nevertheless, though the Greek ontotetês sends us, through Latin translations, to a supposedly atemporal “entity” or to an “essence” that ontology would study, there is no reason (besides tradition) to believe that those entities or essences should be absolute and not asymptotic, governed by partial gluings in a correlative evolution between the world and knowledge. Bimodality, in the sense of Petitot,21 that is, dynamic movement both in physical and morphological-structural space, is related to such a state of things, where “things” have in fact to be replaced by “processes” (functors, natural transformations and adjunctions in mathematical category-theoretic settings, see Section 3). Both prefixes (trans/, bi/) offer a suitable ground to understand the wanderings of contemporary art mathematics.
Charles Sanders Perice22 had already imagined (or discovered, according to our variable ontological commitment) a wonderful phenomenological tool, which helps to unravel the multilayered geometry of the (trans/, bi/) situation. Phaneroscopy, or the study of the phaneron, that is the complete collective spectrum present to the mind, includes the doctrine of Peirce’s cenopythagorean categories, which observe the universal modes (or “tints”) occurring in phenomena. Peirce’s three categories are vague, general, and indeterminate, and can be found simultaneously in every phenomenon. They are interlaced in several levels, but can be prescised (distinguished, separated, detached) following recursive layers of interpretations, in progressively more and more determined contexts. A dialectics between the One and the Many, the universal and the particular, the general and the concrete, is multilayered along a dense variety of theoretical and experimental fibers.
Peirce’s Firstness detects the immediate, the spontaneous, whatever is independent of any conception or reference to something else. Secondness is the category of facts, mutual oppositions, existence, actuality, material fight, action, and reaction in a given world (two uses of the term “category” should not be confused in this article: “category” alone will refer to a philosophical category, following Aristotle; “category-theoretic,” “category theory,” or “mathematical category” will refer to its technical mathematical sense). Thirdness proposes a mediation beyond clashes, a third place where the “one” and the “other” enter a dialogue, the category of sense, representation, synthesis. As Peirce explains:
By the Third, I understand the medium which has its being or peculiarity in connecting the more absolute first and second. The end is second, the means third. A fork in the road is third, it supposes three ways. … The first and second are hard, absolute, and discrete, like yes and no; the perfect third is plastic, relative, and continuous. Every process, and whatever is continuous, involves thirdness. … Action is second, but conduct third. Law as an active force is second, but order and legislation third. Sympathy, flesh and blood, that by which I feel my neighbor’s feelings, contains thirdness. Every kind of sign, representative, or deputy, everything which for any purpose stands instead of something else, whatever is helpful, or mediates between a man and his wish, is a Third.23
Peirce’s vague categories can be “tinctured” with key-words: (1) Firstness: immediacy, first impression, freshness, sensation, unary predicate, monad, chance, possibility; (2) Secondness: action-reaction, effect, resistance, binary relation, dyad, fact, actuality; (3) Thirdness: mediation, order, law, continuity, knowledge, ternary relation, triad, generality, necessity. The three Peircean categories interweave recursively and produce a nested hierarchy of interpretative modulations.24 A series of modes and tones enter the analysis, and, as we shall presently see, when applied to the dialectics (A)-(D) between art and mathematics, the series helps to explain their deep complexity. The interest of Peirce’s method lies in the permanent iterative possibility of his categorical analysis (sequences of the form n.m.p.q … with n, m, p, q ranging through 1, 2, 3—see examples below). The iteration allows, in each contextual level (p, q, …), further and further refinements of previous distinctions obtained in prior levels (m, n, …). Dynamic knowledge yields progressive precision through progressive prescision. Intelligence grows with the definition of more and more contexts of interpretation, and the association of finer and finer cenopythagorean tinctures inside each context.
In Peirce’s triadic classification of the sciences,25 Mathematics is situated in the first branch (1), along the realm of possibilities. Esthetics appears inside Philosophy (2), and, between the Normative Sciences (2.2), it comes as a First (thus Esthetics lies on the site 2.2.1). Art as such does not enter into the space of “sciences”, but it emerges as a web of forms of material creativity—see our first dialectics (A)—which lie on the sites 3.2.2 or 3.2.3 (material mediations, in order to force sense—classic art, or action, contemporary art). As a consequence, following Peirce’s classification of knowledge, mathematics and art constitute again a forceful polarity (1 versus 3.2.3). Now, an inverse vision of the triadic tree affords an interesting transit between art and mathematics. For example, if we place the tree on a sheet (as in Peirce’s existential graphs,26 we look at it from the recto (1) or the verso (3.2.3) of the page, and we transit through cuts and ramification points imagined on the page (which correspond to precise existential graphs calculi in Alpha and Gamma graphs), we are then “admixing” in careful ways reason and sensibility. Iteration and deiteration techniques along the tree are some of Peirce’s major discoveries (with profound consequences in logic, which we cannot expand on here.27 But without delving into too much technical mathematics, we can easily see that the second dialectics (B) between art and mathematics becomes—on the tree—a lattice-theoretic problematic. In fact, on one hand, duality is clearly expressed thanks to the minimum (1) and maximum (3.2.3) numerical indexes of the classification. On another hand, the iteration of mathematics towards art (1→3.2.3), and its inverse deiteration (1←3.2.3), show that a continuous mediating field is stretched between the polarities of art and mathematics, as was presupposed by the third dialectics (C). Finally, strata and residues are well contemplated in Peirce’s architectonics, approaching thus our fourth dialectics (D). Through the very iteration of the cenopythagorean categories, objects and concepts lying in a given stratum (n.m.p.q…) codify and reflect their upper levels (n, n.m, n.m.p, …), revealing both transits and obstructions in the iteration/deiteration processes.
The conceptual and practical back-and-forth between diverse layers is governed by the pragmatic(ist) maxim, which naturally encodes Peirce’s categories. The maxim asserts that we can only attain knowledge after conceiving a wide range of representation possibilities for signs (firstness), after perusing active-reactive contrasts between sub-determinations of those signs (secondness), and after weaving recursive information between the observed semiotic processes (thirdness). The maxim acts as a sheaf with a double support function for the categories: a contrasting function (secondness) to obtain local distinctive hierarchies, and a mediating function (thirdness) to globally unify the different perspectives. In fact, a broad, conceptual differential and integral calculus seems be in action. Peirce imagined a universal lattice of forms to reintegrate the Many into the One, the local into the global, the particular into the universal, the concrete into the abstract. It is a strategy that anticipated some basic goals of mathematical category theory, where apparently different descriptions of objects in diverse concrete mathematical categories (combinatory, logical, topological, algebraic, etc.) are reintegrated through their universal behavior in abstract mathematical categories (spaces of definition governed by the existence-and-uniqueness quantifier ∃!). Art, the second major pole of human thought according to Francastel, inverts the strategy, and differentiates global canvases. Material existence is reified, hoping that concrete residues will reflect abstract totalities.
3. Multilayered Sites and Dynamic Logics
Hesse’s contamination of science and literature in The Glass Bead Game reifies, in the concrete space of a novel, Peirce’s wider synechism (from the Greek syneches, joining together). One of Knecht’s student poems opens up a geometry of elevation: “Traversing spaces and spaces …, the universal spirit does not want to bound us, but to lift us from one degree to another.”28 We are in the presence of a multilayered site, from which multiverse visions can be projected to the diverse strata of the architectonics. Our understanding of contemporary culture has to be situated in such multilevel configurations, emphasizing in particular some key properties: (i) non-separation and continuity, (ii) multiplicity and ramification, (iii) local/global potential gluings. Non-separation and continuity refer, on one side, to a topology not forced by points (Hausdorff spaces), thus to spaces where objects (sets) are replaced by processes (sections in a sheaf); and, on the other side, to the mandatory motto of our epoch: to reintegrate separated, disciplinary knowledge, as The Glass Bead Game novel idealized, and the Glass Bead journal tries to realize. Multiplicity and ramification refer to the dynamic, magmatic forces of diversity and differentiation which impulse creativity.29 Local/global potential gluings refer to the main Transmodern alternative30 which, beyond just local postmodernism, reintegrates fragments, residues, and ruins, in global non-absolute perspectives. Here, the possibility to construct relative universals (apparently a contradiction in terms), has become one of the essential guides of our times (see below). As we will see, a sound completion of these properties leads to dynamic, non-classical logics which govern the different configurations.
Riemann’s theory of functions of complex variable, invented/discovered in his outstanding PhD thesis, incorporate properties (i)-(iii) in precise modes. The thesis, Fundamental principles for a general theory of functions of complex variables,31 introduces new techniques close to (i)-(iii): a double geometric characterization of holomorphic functions, through Cauchy-Riemann equations and conformality—close to (i); Riemann surfaces, in par. V of the thesis, through a description of paths in the surface—close to (ii); and, back-and-forth techniques between global analysis and local expansions, through general integral representation theorems—close to (iii). In simple terms, we may now describe the basic idea beyond a Riemann surface as a partial solution to a Many/One problem. The idea is to represent a multivalent algebraic relation between two complex variables thanks to a multilayered ramification on a continuous surface which turns a many-one relation into a one-one (univalent) relation. Multiplicity is both ramified and glued in a universal surface. The dialectics between discontinuity (many-valuedness, breaks) and continuity (univalence, gluing) is synthesized in a unifying concept.
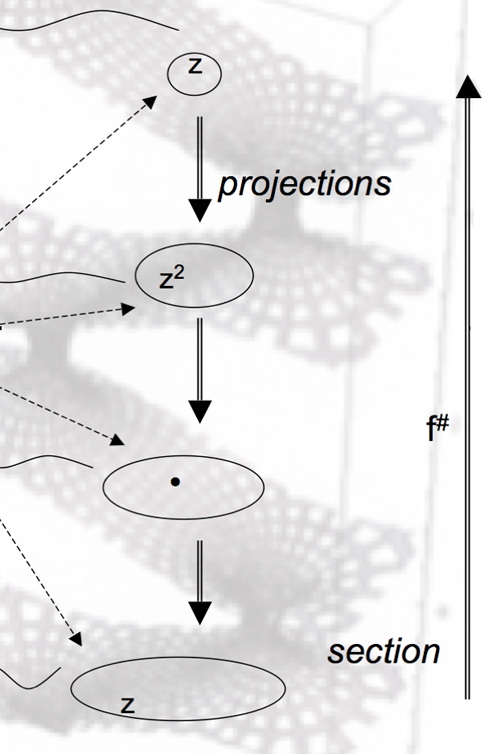
If we could construct Riemann surfaces for fragments of culture, we could be able to describe better the four dialectics (A)-(D) between art and mathematics (the aim of this paper is just to suggest it—no such construction has ever been realized, or even dreamed after Valery.32 33 Indeed, dialectics (A) could then be sub-determined through projections (universal→ particular) and sections/injections (particular→ universal), two natural operations on a Riemann surface (see Figure 1, including modal operators which model Peirce’s Gamma graphs). Dialectics (B) could be imagined through the twists (forms) of the surface, which represent their associated mathematical smoothness (structure). Closer to dialectics (C), the ramification points of the surface (see Figure 1) would be precisely the sites where discreteness deploys into the continuity of the leaves. Finally, according to dialectics (D), the values of a function at isolated points, in each leaf, could be understood as the remainders, or local residues, of the global behavior of the function on the global surface.
As an example, imagine the complexity of Picasso’s Guernica (1937). We can easily observe that the planar surface of the painting is just an accident of the matter involved, and that the painting has really to be deployed through many levels of our imagination. Conceptually and materially, Guernica goes well beyond its driven two dimensions, and it is a wonderful construction of a (bi/, trans/) chef d’oeuvre. Guernica‘s geometry lies on a multilayered site, which recalls a Riemann surface, with many ramification points (sense and esthetic spreaders) available at the very corners of the architectural panels blurred by Picasso34 for amazing textural details on those ramifications). The universality of Picasso’s work rests on the extreme genericity of its particulars: dialectics (A) is at work in its full compassionate force, encoding all human tragedies in a sweeping panorama. Universals are projected, and become really incarnated in our flesh. The interplay of form and structure—dialectics (B)—synthesizes the technical geniality of Guernica. The de/formations of figures and animals reveal the de/structuration of panic, death, and sorrow. Imagine that you could project them on moving, dynamic Riemann surfaces (as our mind does with local particulars, wounded mouths, hands, wrists): the pain drawn in a cut or a flame, would be projected into our grief, in turn projected into universal affliction. Following dialectics (C), the singular and the discrete would be mathematically part of the universal and the continuous—as they already are artistically. Finally, another of Guernica‘s supreme artistic achievements resides in the complex interplay between local residues (explicit death ruins) and the global destroyed environment (Basque life)—a form of dialectics (D). Guernica‘s artistic force is completely exceptional, certainly self-contained, but we can see that a dual, conceptual, multilevel geometric synthesis, can also extend its abundant, never-ending polysemous richness.
The eventual interest for culture of modern (1830-1950) and contemporary (1950-today) mathematics consists, not in the partial modelings that mathematics may offer, but rather in its help to deploy imagination. Riemann surfaces stimulate visual and conceptual inventiveness. Looking at them (and handling them; they are beautiful material constructs) allows transits and possibilities that rigid, classical, non-plastic geometries would prevent. In a similar vein, Grothendieck toposes (categories equivalent to categories of sheaves over abstract topologies, 1962) constitute plastic sites, specifically open to dynamic variations. Grothendieck toposes unify deep insights on arithmetic (number) and geometry (form)35. Beyond Cantorian, classical, static sets, the objects in a topos are to be understood as generalizations of variable sets (see Figure 2). Instead of living over a rigid bottom, governed by classical logic, they live over a dynamic Kripke model, governed by intuitionistic logic. Beyond the classical example of the separated sheaf of holomorphic functions, a sheaf does not have to be separated in a general topos: points do not have to determine their associated objects. We can even imagine objects without points, defined only through flux processes. A wonderful example is the topos of actions of monoids. Such a topos has an underlying classical logic (where the law of excluded middle holds and points are essential) if and only if the monoid is a group. Thus, when we deal with structures which are monoid non-groups, the logic of their action is just intuitionistic, non-separated, closer to topological fluxions, deformations, disruptions.
In a simple motto, we may characterize Grothendieck as the greatest mathematician who, after Poincaré, unified Galois and Riemann, the two mathematical geniuses of the nineteenth century.37 We may thus imagine that, on a conceptual, non-exclusively technical level, Grothendieck toposes generalize Riemann surfaces in some way. Even if the assertion is not mathematically correct (we would have to introduce also Grothendieck’s schemes into the account), methodologically it is fruitful. Figure 1 and Figure 2 show dynamic, relative movements. Bases change, no eternal objects are considered. But the correlative changes are in turn studied mathematically, and they are incorporated as new objects in an upper level. In this way, an iterated dynamics emergesa dynamical study of dynamics—which can have a strong influence in cultural studies.
As another example, going a little further and inverting again our thought, one can deal with toposes whose underlying logics are dual to intuitionistic logic. Paraconsistent logics (1963) thus appear in the panorama, logics where we can have local contradictions without forcing global contradictions which would destroy the system.38 It is fairly clear that the dynamic logics of art are either intuitionistic or paraconsistent, but certainly not classical. The dialectics of art and mathematics (A)-(D) already hinted at such a situation, but it is interesting to notice that, (1) if we situate ourselves in a multilayered site akin to art, that is, in some sort of non-well-defined Grothendieck topos of art actions (compare with the well-defined topos of monoid actions), (2) if we think dually—as art should do with respect to mathematics, and (3) if we allow ourselves to live in a continuous medium of contradictions, then we will be approaching many of the strongest forms of contemporary art (as in Caro, Kabakov, or Kiefer39).
Of course—going against the usual captions which inform us about fictional characters when films finish—we may assert that our indexing (1)-(3) in the last paragraph is Peircean, and it is certainly not accidental. Worse: if we read well, The Glass Bead Game must have listed already this combinatory possibility in one of its infinite game versions.