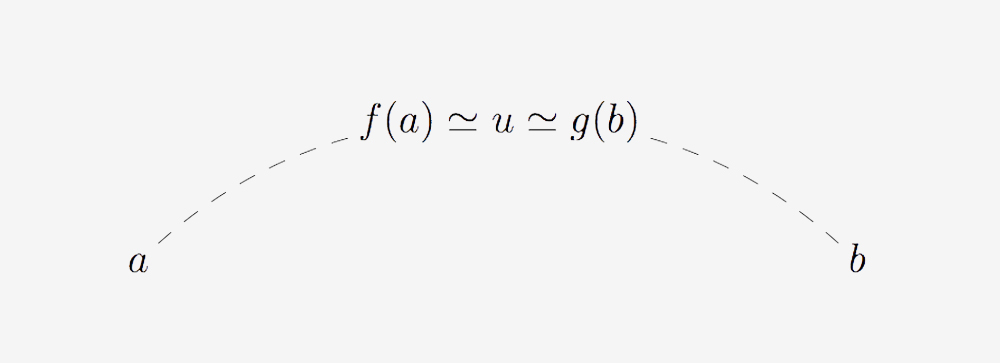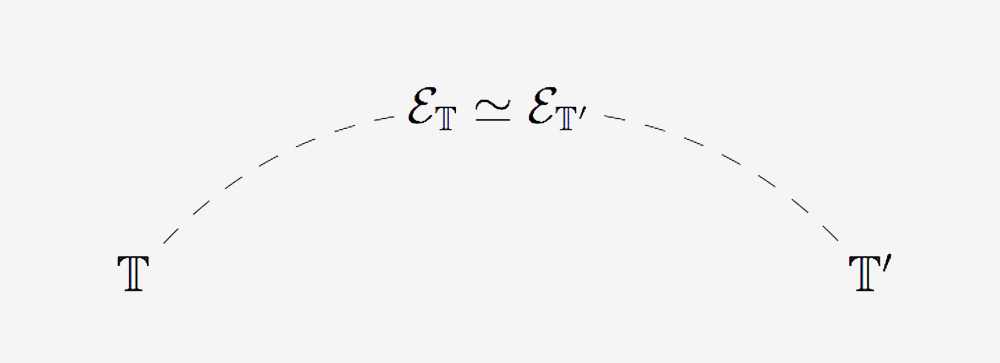Les mathématiques se divisent en plusieurs domaines distincts : géométrie, théorie des nombres, algèbre, analyse, logique mathématique, etc. Au fil des ans, chacun d’eux a évolué en développant ses propres idées et techniques pour atteindre le remarquable degré de spécialisation qu’on leur connaît. Aujourd’hui plus encore que par le passé, nous ressentons le besoin de théories unificatrices qui pourraient relier les différents domaines des mathématiques et les divers ensembles de concepts, objets et méthodes qui leur sont associés, de façon nouvelle et efficace. Ainsi disposerions-nous de nouveaux outils pour résoudre des problèmes qui se posent depuis longtemps. À plusieurs reprises déjà, des solutions à des problèmes profonds existant dans un champ donné ont été trouvées en utilisant d’abord, voire uniquement, des méthodes appartenant à d’autres champs – ce qui montre bien qu’on devrait plutôt considérer les mathématiques comme un tout cohérent que comme une série de champs séparés. Qu’on pense par exemple à la géométrie analytique, qui permet d’étudier des formes géométriques grâce à la manipulation algébrique, ou à la notion grothendieckienne de spectre, qui permet d’étudier des objets discrets grâce à une intuition géométrique continue.
L’importance des « ponts » entre différents domaines tient au fait qu’ils permettent de transférer des connaissances et des méthodes entre ces domaines de telle manière que les problèmes formulés dans le langage d’un domaine donné peuvent être étudiés, et éventuellement résolus, en utilisant des techniques appartenant à un domaine différent, et que les résultats d’un domaine donné peuvent être transférés de façon appropriée en résultats dans un autre domaine.
La théorie des topos de Grothendieck peut fournir un moyen efficace d’unifier entre elles différentes théories mathématiques. Plus précisément, la possibilité de représenter des topos de manières multiples peut être exploitée pour construire des « ponts » reliant différentes théories et permettant un transfert d’information entre elles.
Les topos sont des concepts logiques abstraits qui se situent à un niveau de généralité idéal pour éclairer l’ensemble des mathématiques. À toute théorie mathématique de forme très générale (relevant de l’algèbre, de la géométrie, ou d’autre domaine des mathématiques) peut être associé un topos, appelé topos « classifiant » de cette théorie, qui renferme ses caractéristiques essentielles (c’est-à-dire précisément celles qui sont invariantes relativement à une notion générale d’équivalence des théories). Cela nous permet d’étudier des théories via leurs topos classifiants. Différentes théories peuvent être classifiées par le même topos, ce qui signifie précisément qu’elles décrivent, dans des langages différents, les mêmes structures. L’existence de différentes théories classifiées par le même topos se traduit, au niveau technique, par l’existence de multiples représentations pour ce topos. Ce dernier peut alors être utilisé comme un « pont » permettant de transférer des propriétés, des idées et des résultats entre ces théories.
Au cours des dernières années, nous avons développé un ensemble de méthodes et de techniques interdisciplinaires afin d’utiliser de manière efficace les topos comme des « ponts » unifiants. Ce faisant, nous avons mis au jour un certain nombre de connexions entre différentes théories mathématiques qui étaient jusqu’alors cachées, voire, dans de nombreux cas, insoupçonnées. Notre intuition a été soutenue dès 2009 par de premiers résultats puis confortée année après année par de nouveau développements dont certains fournirent la solution à des problèmes qui se posaient depuis longtemps. Depuis lors s’est constitué un corpus de résultats mathématiques, comprenant un certain nombre d’applications dans des champs distincts tels que l’algèbre, la géométrie, la topologie, l’analyse fonctionnelle, la théorie des modèles et la théorie des preuves.
Le propos de cet article est de fournir une introduction conceptuelle accessible à des non spécialistes de la théorie des « ponts » de la théorie des topos comme “ponts”1. Le dernier paragraphe est plus technique que les précédents et requiert, pour être compris correctement, un minimum de familiarité avec la logique et la théorie des catégories2.
Le concept d’unification
Avant de poursuivre, il convient de clarifier la signification du terme « unification ». En effet, ce terme est légèrement ambigu et peut recouvrir diverses significations.
Unification « statique » et unification « dynamique »
On peut distinguer deux types d’unification :
– l’unification « statique » (par voie de généralisation) : deux concepts sont considérés comme des cas particuliers d’un concept plus général
Les résultats qui s’appliquent au concept général peuvent être spécialisés pour produire des résultats sur les deux autres concepts plus particuliers.
– l’unification « dynamique » (par voie de construction) : deux objets sont associés l’un à l’autre par le biais d’un troisième (généralement construit à partir d’eux), qui agit comme un « pont » permettant de transférer de l’information entre eux :
Le transfert d’information provient du processus consistant à « traduire » des propriétés (resp. constructions) sur l’ « objet pont » en propriétés (resp. constructions) sur les deux objets.
Nous qualifions la première forme d’unification de « statique » en vertu du fait que réaliser deux concepts différents comme cas particuliers d’un concept plus général n’offre pas en soi une manière de transférer de l’information entre eux. Par exemple, le fait que les préordres et les groupes soient tous deux des exemples particuliers de la notion générale de catégorie n’offre pas en soi un moyen de transférer des résultats concernant les préordres à des résultats concernant les groupes ou vice-et-versa.
En revanche, la seconde forme d’unification permet un transfert « dynamique » d’information entre les deux objets donnés. En effet, le troisième objet qui est associé à chacun des deux objets, ou construit à partir d’eux, admet deux « représentations » différentes correspondant aux deux manières de le construire à partir de chacun de ces deux objets. Un tel objet constitue ainsi un « pont » entre les deux objets donnés au sens où de l’information peut être transférée entre eux en traduisant des propriétés de (resp. des constructions sur) l’objet pont en propriétés des (resp. constructions sur les) deux objets en exploitant ses deux représentations différentes.
Illustrons la différence entre ces deux types d’unification au moyen de quelques exemples mathématiques.
En offrant un système où tous les concepts mathématiques usuels peuvent être exprimés de manière rigoureuse, la théorie des ensembles a représenté la première tentative sérieuse de la logique pour unifier les mathématiques, du moins au niveau du langage. Plus tard, la théorie des catégories a offert un langage abstrait alternatif grâce auquel la plus grande partie des mathématiques peut être formulée. À cet égard, cette théorie a représenté un pas de plus vers l’objectif d’une « unification des mathématiques ». Quoi qu’il en soit, ces deux systèmes réalisent une unification « statique » en ceci que, si chacun d’eux offre une manière d’exprimer et d’organiser les mathématiques en un seul langage, ils n’offrent pas en eux-mêmes de méthodes efficaces pour un réel transfert de connaissances entre des champs distincts.
En revanche, la théorie des topos comme « ponts » offre une manière systématique de comparer des théories mathématiques distinctes et de transférer entre elles des connaissances. Dans ce cadre, les deux objets devant être associés l’un à l’autre sont des théories mathématiques distinctes qui partagent un « noyau sémantique » commun, tandis que l’objet pont est un topos de Grothendieck représentant précisément ce « noyau » commun.
De même qu’en général un « objet pont » donné peut relier non seulement deux objets entre eux mais aussi plusieurs paires différentes d’objets, il existe dans le cadre de la théorie des topos, pour chaque topos, un nombre infini de théories mathématiques différentes qui lui sont associées (à travers la construction du topos classifiant).
D’autres exemples d’unification dynamique se rencontrent bien sûr en mathématiques ; en fait, les invariants sont toujours sources de « ponts » entre les objets à partir desquels ils sont définis. Le groupe fondamental d’un espace topologique, par exemple, peut être utilisé comme un pont pour transférer de l’information entre des espaces topologiques, au sens où si deux espaces topologiques ont des groupes fondamentaux isomorphiques, alors certaines propriétés topologiques, telle que la connexité simple, peuvent être transférées le long de ces espaces ; de la même manière, des groupes peuvent être utilisés pour classifier des géométries comme dans le programme d’Erlangen de Klein3, etc.
L’aspect surprenant des topos est que, contrairement à la plupart des invariants considérés en mathématiques, ils permettent de comparer, et de relier entre elles de manière efficace, des théories mathématiques pouvant éventuellement appartenir à différents sous-domaines des mathématiques.
L’idée de « pont »
En général, on compare des paires d’objets entre lesquelles il existe une forme de relation. Pour transférer de l’information entre des objets associés par une relation donnée, il est donc fondamental d’identifier (et, si possible, de classifier) les propriétés des objets qui sont invariantes via cette relation. Selon les cas, cette tâche peut être ou bien aisément réalisable ou d’une incroyable difficulté. En fait, une relation entre deux objets donnés est en général une entité abstraite relevant d’un contexte théorique qui est normalement différent de celui dans lequel se situent ces deux objets. Ainsi devient-il d’une importance cruciale d’identifier des entités concrètes qui pourraient fonctionner comme des « ponts » reliant deux objets donnés.
On peut penser à un objet pont reliant deux objets a et b comme à un objet u qui peut être « construit » à partir de n’importe lequel de ces deux objets a et b et qui admet deux représentations différentes f(a) et g(b) associées par une quelconque équivalence ≃, la première représentation étant dans les termes de l’objet a et la seconde dans les termes de l’objet b :
Les transferts d’information proviennent du processus consistant à « traduire » ≃- invariantes (resp. constructions) sur l’ « objet pont » en propriétés (resp. constructions) sur les deux objets a et b en utilisant les deux différentes représentations de u. On notera que l’invariance par rapport à ≃ est essentielle pour pouvoir considérer la propriété donnée de (ou construction sur) u à la fois du point de vue de a, en utilisant f, et du point de vue de b, en utilisant g.
Bien sûr, un « pont » de ce type est plus ou moins utile suivant que les « encodages » f et g se comportent plus ou moins bien pour permettre d’authentiques « décodages » de la propriété donnée de (ou de la construction sur) f(a) (resp. g(b)) dans les termes des propriétés de (ou des constructions sur) a (resp. de/sur b).
L’idée de « pont » est étroitement associée à celle de « construction invariante ». Étant donné deux ensembles I et O, et deux relations d’équivalence ≃I et ≃O respectivement sur I et sur O, on peut définir une construction invariante f : (I,≃I) → (O, ≃O ) comme une fonction f : I → O qui respecte les relations d’équivalence (c’est-à-dire telle qu’à chaque fois que x ≃I y, f(x) ≃O f(y)). On dira que f est conservative si elle reflète les relations d’équivalence (c’est-à-dire qu’à chaque fois que f(x) ≃O f(y), x ≃I y). Étant donné une construction invariante f : (I,≃I) → (O,≃O), un objet pont reliant deux objets x et y de I est un objet b de O tel que b ≃O f(x) et que b ≃O f(y). Étant donné une construction invariante conservative f : (I,≃I) → (O,≃O ), les objets ponts dans O, considérés à ≃O équivalence près, peuvent être pensés comme des objets classifiants, dans la mesure où ils peuvent être pris comme des représentants canoniques de ≃I classes d’équivalence.
Bien sûr, un « pont » de ce type est particulièrement utile pour classifier les propriétés invariantes par ≃I dans les cas où il est plus facile de travailler avec des objets de type O qu’avec des objets de type I, ou lorsque la relation ≃O est plus malléable que la relation ≃I.
Comme nous le verrons dans le paragraphe 4, dans le contexte de la théorie des topos comme « ponts », les objets à comparer entre eux sont des théories mathématiques (formalisées au sein d’un type de logique du premier ordre) tandis que la construction invariante est donnée par la construction du topos classifiant.
Traductions structurelles
La technique des ponts peut être interprétée d’un point de vue linguistique comme une méthodologie pour traduire des concepts d’un contexte à un autre. Mais de quel genre de traduction s’agit-il ? En général, on peut distinguer entre deux approches fondamentalement différentes de la traduction.
– l’approche « axée sur le dictionnaire » ou « ascendante », qui consiste à renommer les seuls mots qui composent les phrases en ayant recours au dictionnaire.
– l’approche « axée sur les invariants » ou « descendante », qui consiste à identifier des concepts appropriés qui devront rester invariants dans la traduction et à analyser ensuite la façon dont ces invariants peuvent être exprimés dans les deux langages.
Comme on peut naturellement s’y attendre, les traductions de la première catégorie, bien que parfois utiles, restent fondamentalement superficielles en ceci qu’elles ne modifient pas la « forme » des phrases sur lesquelles elles interviennent et n’offrent donc pas de façons réellement différentes de véhiculer un certain message. En revanche, les traductions axées sur les invariants sont susceptibles de transformer considérablement la forme syntaxique utilisée pour exprimer une certaine signification, et d’ouvrir ainsi de nouvelles perspectives et points de vue sur le message donné. Nous y reviendrons dans la sous-partie 3.2.
Les traductions d’une théorie mathématique à une autre réalisées par le biais de bi-interprétations entre elles appartiennent à la première catégorie. En effet, la bi-interprétation fonctionne comme une sorte de dictionnaire permettant de traduire des formules écrites dans le langage de la première théorie en formules écrites dans le langage de la seconde. En revanche, les traductions « axées sur les ponts », et en particulier celles de la théorie des topos, appartiennent à la seconde catégorie. En fait, dans le contexte de la théorie des topos comme « ponts », les propriétés invariantes sont des invariants de la théorie des topos, et l’expression de ces invariants dans les termes des deux théories différentes est essentiellement déterminée par la relation structurale entre le topos et ses deux représentations différentes.
Quelques exemples de « ponts » en science.
Afin d’illustrer le concept de « pont » tel que nous l’avons présenté, étudions maintenant quelques situations scientifiques pouvant être naturellement interprétées en termes de « ponts ».
L’astronomie : l’ « étoile classifiante » d’une planète
L’univers est composé de plusieurs étoiles, autour desquelles certains corps, appelés planètes, sont en rotation. Différentes planètes peuvent être en rotation autour d’une étoile donnée, mais chaque planète est en rotation autour d’une seule étoile, que nous appelons l’étoile « classifiante » de cette planète.
La trajectoire qu’effectue une planète donnée autour de son étoile classifiante est déterminée par deux ensembles d’éléments : les paramètres déterminant l’ellipse et la période de révolution autour de son étoile classifiante. La paire (les paramètres de l’ellipse, la période de révolution) d’une planète donnée détermine son orbite et son étoile classifiante.
Une étoile classifiante ne peut être identifiée depuis l’une des planètes qu’elle permet de classifier (et de manière équivalente, depuis la paire associée à cette planète) et représente le « bon » point de vue depuis lequel on doit l’observer (de fait, le mouvement elliptique d’une planète paraît très étrange lorsqu’on l’observe de tout autre point de vue que celui de ses foyers).
Différentes planètes en rotation autour de la même étoile peuvent être étudiées en relation les unes aux autres en utilisant les propriétés de leur étoile classifiante commune, laquelle fonctionne par conséquent comme un « objet pont » venant les relier. En effet, il existe des relations naturelles entre les propriétés des planètes et celles des étoiles autour desquelles elles tournent.
Pour nous faire une idée de l’utilisation des « ponts » en astronomie, prenons par exemple les lois de Kepler. La propriété selon laquelle toutes les planètes en rotation autour d’une étoile donnée ont des orbites de forme elliptique peut être considérée comme une propriété invariante des étoiles (ou, plus généralement, des corps autour desquels d’autres corps sont en rotation). L’orbite concrète d’une planète donnée peut être considéré comme dérivant du processus consistant à exprimer l’invariant abstrait « les orbites sont elliptiques » dans les termes de la paire concrète associée à cette planète donnée. Ainsi les formes des orbites de deux planètes distinctes autour de la même étoile représentent-elles différents exemples d’un seul modèle abstrait.
Par ailleurs, il n’est pas rare que l’étude des caractéristiques d’une planète donnée permette d’inférer certaines propriétés de son étoile classifiante, et que ces propriétés puissent à leur tour « se réfléchir » [« reflected back »] en propriétés d’une autre planète en rotation autour de la même étoile. Par exemple, la troisième loi de Kepler affirme que le quotient du carré de la période orbitale d’une planète par le cube du demi-axe majeur de son orbite est une constante qui est propre à l’étoile et ne dépend pas de la planète donnée. Ce principe peut ainsi être considéré comme une propriété invariante des étoiles (ou, plus généralement, des corps autour desquels d’autres corps sont en rotation), et les trajectoires concrètes effectuées par les planètes peuvent être interprétées comme différentes manifestations de cette propriété abstraite dans le contexte des planètes distinctes (ou des paires qui leur sont associées). L’étoile classifiante commune peut ainsi être utilisée comme un « pont » pour transférer de l’information entre deux planètes ; en effet, l’étude de la trajectoire concrète d’une planète permet d’inférer la constante propre de son étoile classifiante, et cette information contraint en retour la trajectoire concrète de n’importe quelle planète en rotation autour d’elle.
La linguistique : des « ponts » pour traduire
Une des caractéristiques fondamentales de la traduction est l’ensemble des propriétés abstraites du texte (par exemple la « signification », la « musicalité », les caractéristiques « structurelles », etc.) qu’elle garde invariantes.
Une traduction littérale adopte une approche axée sur le dictionnaire, ou ascendante, dans la mesure où elle consiste, en gros, à diviser le texte en phrases puis en mots ou en expressions courtes, à remplacer chaque mot (resp. courte expression) du premier langage par un mot (resp. courte expression) écrit dans l’autre langage qui lui correspond selon un dictionnaire donné, et enfin à assembler ces mots « de manière ascendante » en suivant une structure grammaticale, sinon identique, du moins semblable, à celle selon laquelle les mots (resp. courtes expressions) d’origine correspondant étaient disposés dans le texte. À partir de cette description, il est clair que ce qui est préservé par ce type de traduction est la structure syntaxique des phrases qui composent les textes, mais pas nécessairement la signification ou la musicalité des textes, ce qu’on serait pourtant en droit d’attendre d’une bonne traduction. Voilà pourquoi les traductions automatiques ou littérales ne sont pas toujours possibles, et lorsqu’elles le sont, s’avèrent souvent très insatisfaisantes, surtout lorsqu’elles impliquent deux langages possédant des façons syntaxiques radicalement différentes d’exprimer une signification donnée.
Ce qui soulève naturellement la question suivante : quel type d’approche doit-on adopter pour obtenir une bonne traduction ? Contrairement à une traduction littérale, une bonne traduction doit procéder d’une manière descendante, ou axée sur les invariants, en commençant par identifier un ensemble de propriétés abstraites des textes qu’on souhaite voir demeurer invariantes dans la traduction, puis en utilisant ces propriétés P (ou l’ « intersection » de toutes ces propriétés) comme un « pont » pour traduire d’un langage à l’autre, comme suit. Pour chacune de ces P, on considère la meilleure manière d’exprimer P dans le premier langage, puis la meilleure manière dont P peut être véhiculé dans le second langage ; les expressions qui en résultent du fait de la traduction sont alors vouées à se correspondre entre elles. On notera que dans une traduction de ce type, ce n’est pas nécessairement la structure syntactique qui est préservée, comme dans le cas de la traduction littérale, mais les propriétés qui sont fixées au début comme étant celles qu’on désire voir rester invariantes.
Une traduction littérale n’est ni particulièrement intéressante, ni profonde d’un point de vue conceptuel, en ceci qu’elle consiste essentiellement à renommer ou ré-étiqueter les composants premiers d’un texte en fonction d’un dictionnaire. En revanche, une bonne traduction, littéraire, est souvent une œuvre d’art. Elle peut révéler de nouveaux aspects du texte qui étaient en un sens « cachés » dans la version originale et permettre ainsi des interprétations nouvelles et différentes du message que contenait cette première version.
Génétique : l’ADN considéré comme un « pont »
L’ADN (humain) renferme de nombreuses caractéristiques essentielles de l’individu auquel il appartient, mais il est invariant quant aux caractéristiques contingentes de cet individu, comme son apparence physique à un moment donné (ou son âge). C’est l’individu qui détermine quasi uniquement son ADN, mais il existe de très nombreuses manières d’extraire cet ADN (de différentes parties du corps, par exemple). Plusieurs caractéristiques spécifiques des individus se reflètent dans des caractéristiques particulières de leur ADN – ce qui fait de l’ADN un objet particulièrement apte à fonctionner comme un « pont » pour transférer de l’information entre différents individus. Par exemple, la découverte de similarités entre l’ADN de divers individus peut révéler des relations de parenté biologiques entre eux ou des dispositions communes à certaines maladies. On notera que le genre de découvertes que peut permettre une analyse d’ADN ne peut être atteint par d’autres méthodes : adopter ce niveau d’analyse est en effet nécessaire pour dévoiler les caractéristiques « cachées » des individus encodées dans l’ADN.
On observe la même chose dans la théorie des topos : la notion de topos classifiant d’une théorie donnée joue le rôle d’une sorte d’ADN de cette théorie, dont l’étude peut révéler des aspects de cette théorie qui sont à peine visibles lorsqu’on adopte des techniques alternatives. De la même manière qu’en génétique on étudie la façon dont les modifications de l’ADN influencent les caractéristiques d’un individu, dans la théorie des topos, on peut étudier l’effet que des opérations sur les topos ont sur les théories qu’ils classifient.
Idéal = réel ?
Les ponts abondent en mathématiques et dans d’autres champs scientifiques et peuvent être considérés comme « responsables » (au moins de manière abstraite) de la « genèse » des choses et de la nature de la réalité telle que nous la percevons. L’idée de pont est une abstraction, mais les ponts issus des sciences expérimentales peuvent souvent être identifiés à des objets physiques réels. En fait, les situations les plus instructives surviennent lorsque ces objets idéaux admettent des représentations « concrètes », ce qui nous permet de contempler la dynamique de « différenciation à partir de l’unité » dans tous ses aspects. Les topos de Grothendieck nous permettent de matérialiser un nombre gigantesque d’objets idéaux et de jeter ainsi des ponts efficaces entre une grande variété de contextes différents. En général, chercher des représentations « concrètes » de (ou des façons de réaliser) de « concepts imaginaires » peut mener à la découverte d’environnements plus « symétriques » où les phénomènes peuvent être décrits de manière naturelle et unifiée.
Les topos considérés comme des « ponts »
Maintenant que nous avons extrait les caractéristiques conceptuelles essentielles de la technique des « ponts », nous pouvons illustrer sa mise en application dans le contexte de la théorie des topos.
Méthodologie générale
Notre théorie des « ponts » est fondée sur le concept de topos est centrée autour du concept de topos de Grothendieck4. La théorie des topos de Grothendieck est écrite dans un langage catégorique, mais contrairement à la théorie des catégories, elle est bien plus expressive, ce qui est dû à un degré de liberté supérieur inhérent à la définition des topos. En effet, une catégorie peut être pensée comme une paire d’ensembles associés par une structure quelconque répondant à certaines propriétés ; n’importe quel ensemble peut être considéré comme une catégorie, mais la plupart des catégories issues des mathématiques ne sont pas de cette forme. En fait, le concept de topos possède par rapport à la notion de catégorie un degré de liberté supplémentaire.
Les topos sont des objets mathématiques construits à partir d’une paire, appelée site, consistant en une catégorie C et en une notion généralisée de recouvrement J appelée topologie de Grothendieck. Le processus qui produit un topos à partir d’un site donné peut être décrit comme une sorte de « complétion » par rapport à certaines opérations catégoriques relativement auxquelles la catégorie C peut ne pas être complète. D’un point de vue formel, un topos est défini comme une catégorie Sh(C,J) de faisceaux sur un site (C,J).
Différents recouvrements peuvent être considérés sur une catégorie donnée menant en général à des topos inéquivalents, ce qui confère à la notion de topos un degré supplémentaire de liberté par rapport à celle de catégorie. L’existence de ces trois « degrés de liberté » implicite dans le concept de topos (deux pour la notion de catégorie et un pour celle de la topologie de Grothendieck) peut être exploitée pour construire des « univers mathématiques » dans lesquels les théories mathématiques trouvent leur foyer naturel et peuvent être comparées entre elles de manière efficace.
En fait, grâce au travail novateur de Makkai et Reyes dans les années 19705, à toute théorie mathématique T d’un type extrêmement général appelé « géométrique » peut être associé canoniquement un topos appelé topos classifiant de T, qui représente le cadre naturel dans lequel la théorie devrait être étudiée, à la fois en elle-même et en relation avec d’autres théories. Deux théories possédant les mêmes topos classifiants (à équivalence près) sont dites « équivalentes au sens de Morita » ou « Morita-équivalentes ».
L’existence de théories « Morita-équivalentes » l’une à l’autre se traduit, au niveau des sites, par l’existence de différents sites engendrant le même topos (à équivalence près) ; en effet, à toute théorie peut être associé un site tel que le topos construit à partir de celui-ci peut être identifié à son topos classifiant.
Le topos classifiant d’une théorie peut être utilisé de manière efficace comme un « pont » pour transférer de l’information entre cette théorie et une autre théorie « Morita-équivalente » à elle, comme suit. Pour toute propriété ou construction de topos donnée qui est invariante relativement à l’équivalence des topos (cette invariance est requise car le topos classifiant n’est déterminé qu’à équivalence près), on essaie de l’exprimer d’abord dans les termes d’une théorie, puis dans les termes de l’autre ; à condition d’obtenir des caractérisations appropriées reliant les propriétés des théories et les propriétés de leurs topos classifiants (et de manière équivalente, les caractérisations reliant des propriétés de sites et des propriétés de topos), cela conduira à une relation logique entre des propriétés des deux théories écrites dans leur langage respectif :
D’un point de vue technique, le transfert d’information entre les deux théories est réalisé en leur associant des sites qui définissent leur topos classifiant, et en exprimant des invariants de la théorie du topos classifiant commun dans les termes de ces deux sites.
Au-delà de son niveau de généralité (car elle peut être appliquée à des théories mathématiques appartenant à peu près à n’importe quel champ des mathématiques), un des aspects étonnants de cette technique est qu’elle peut être automatisée dans de nombreux cas. En effet, en utilisant les méthodes de la théorie des topos, on peut obtenir des caractérisations du type étudié ci-dessus pour plusieurs invariants, valant de manière uniforme pour n’importe quelle théorie ou du moins pour de nombreuses classes de théories (et pour certaines classes d’invariants, des caractérisations de ce type peuvent même être établies de manière purement mécanique) ; en présence d’une équivalence de Morita, ces caractérisations seront ainsi capables de fonctionner comme les « arches » d’un « pont » reliant les deux théories, ce qui permettra de transférer de l’information entre elles.
Comme on peut naturellement s’y attendre, les traductions entre des propriétés de théories Morita-équivalentes réalisées au moyen de la technique des « ponts » peuvent être très surprenantes. En effet, une propriété invariante abstraite unique définie au niveau de la théorie des topos peut être exprimée de manières complètement différentes dans les termes de différents sites de définition d’un topos donné. Pour prendre un exemple, considérons la propriété de complétude d’une théorie : une théorie géométrique est dite complète si chaque affirmation géométrique écrite dans son langage peut être soit démontrée comme vraie soit démontrée comme fausse dans cette théorie. En général, prouver qu’une théorie est complète est très difficile. Néanmoins cette propriété est équivalente à une propriété invariante simple du topos classifiant (à savoir la propriété du topos d’être bivalent), admettant des reformulations alternatives dans les termes d’autres sites de définition.
Par exemple6, cette propriété invariante est équivalente à la propriété de plongement conjoint sur une catégorie C (c’est-à-dire la propriété selon laquelle deux objets quelconques de cette catégorie peuvent être reliés à un troisième) dans le cas d’un site atomique non trivial ( Cop,Jat) (rappelons que la topologie atomique Jat sur l’opposé d’une catégorie C répondant à la propriété d’amalgamation est la topologie de Grothendieck ayant précisément comme cribles couvrants les cribles non vides). En général, la propriété de plongement conjoint sur une catégorie est une manière bien plus simple à vérifier que la propriété de complétude d’une théorie ; néanmoins, pour les théories T dont le topos classifiant est un topos de faisceaux sur un site atomique non trivial (Cop,Jat), les deux propriétés de complétude de T et la propriété de plongement conjoint de C correspondent l’une à l’autre relativement par un « pont », topos-théorique, ce qui permet de démontrer l’une par l’autre7.
Pourquoi les topos ?
On pourrait se demander pourquoi les topos de Grothendieck jouent si efficacement le rôle de « ponts » pour relier différentes théories mathématiques entre elles. Plusieurs raisons l’expliquent, qui peuvent se résumer de la manière suivante :
– généralité : contrairement à la plupart des invariants utilisés en mathématiques, le niveau de généralité des invariants de la théorie des topos est tel qu’ils conviennent pour comparer entre elles des théories mathématiques (du premier ordre) de tout type ou presque.
– expressivité : de nombreux invariants importants issus des mathématiques peuvent être exprimés comme des invariants de la théorie des topos.
– centralité : le fait que les invariants de la théorie des topos se spécialisent souvent dans d’importantes propriétés ou constructions d’intérêt logique ou mathématique naturel indique clairement la centralité de ces concepts en mathématiques. En fait, tout ce qui arrive au niveau des topos a des ramifications « uniformes » dans l’ensemble des mathématiques.
– flexibilité technique : les topos sont des univers mathématiques très riches en termes de structure interne ; de plus, ils possèdent une théorie des représentations très bonne qui les rend extrêmement efficaces computationellement lorsqu’ils sont considérés comme des « ponts ».