Heralded as “the most important event of the Renaissance”, the invention of linear perspective in the Italian quattrocento occupies a pivotal role in the intertwined processes of rationalization of vision and mathematization of space that constitutes one of the defining features of historical modernity.1 This process has unlocked formidable new sources of human knowledge and power over the world. Yet it also has simultaneously propelled a movement disembedding the activities of perception and spatial reasoning from their exclusive biological substrate to relocate them in various technical apparatuses. Thus the new capacities for human agency brought forth by linear perspective are coeval with the advent of an artificial eye that supplants the primacy of its model.
Much more than a mere internal development within the history of art, linear perspective sits at the confluence of the fields of geometrical optics, pictorial representation, and land surveying. At its heart is a geometric conception of vision that accounts for the natural ocular estimation of spatial distances and begets an array of mathematical techniques and associated instruments for precise measurement by the human eye. A rigorous procedure for the rule-governed (i.e. automatable) construction of images that convey an optically convincing depiction of physical space follows from it. And in common with the field of cartography emerging at the same time, perspective employs a system of geometric projection of a three-dimensional space upon a two-dimensional surface in a manner that preserves the space’s relative proportions and the objects contained within.
In ordering visual space according to “an abstract uniform system of linear coordinates,” perspective binds subjective perception and objective spatial extension through mathematical convertibility.2 For William Ivins, perspective offers in this way a “practical means for securing a rigorous two-way, or reciprocal, metrical relationship between the shapes of objects as definitely located in space and their pictorial representations.”3 Bruno Latour further points to the paramount importance of the “optical consistency” found in Renaissance techniques of visualization for the development of modern scientific culture. Common to linear perspective, scientific mapping, and technical drawings, optical consistency permits the description of physical spaces and objects in a systematic geometric fashion that facilitates the circulation of these representations and allows for “the possibility of going from one type of visual trace to another.”4 These particular representations possess, for Latour, the character of “immutable mobiles” able to disseminate widely and undergo rule-bound transformations and additions without losing or distorting their valuable informational content. These new itinerant forms of inscription not only serve as repositories of accumulated knowledge but as material anchors for the cognitive operations necessary to the emergence and sustenance of a modern scientific culture.5 While these properties do not flow exclusively from it, linear perspective is nonetheless paradigmatic by virtue of “its logical recognition of internal invariances through all the transformations produced by changes in spatial location.”6
If optically consistent visualizations have decisively contributed to the success and proliferation of modern scientific practices, they can be considered more generally as instruments of power for shaping the natural and social world. From the outset, perspective participated in an objectivization of perception, no longer solely residing in phenomenological embodiment but instead now the outcome of a systematic application of “a rational and repeatable procedure.”7 Moreover, this algorithmic apprehension of perception made possible its comprehensive mechanization and relocation within new socio-technical assemblages. Neither perspective nor its associated machines faithfully replicate human vision, of course. The roving, binocular, and psychologically conditioned sight of humans is substituted for a fixed, monocular, and strictly geometric gaze. Yet it is this disembodied and rationalized mode of perception that increasingly prevails and imposes itself on the human sensorium. Or as Ken Hillis puts it, “the body-as-object (and by extension humanity) becomes subject to, even inscribed by, the laws of technique that are intended to render nature more subject to human control.”8
The Rationalization of Vision
In precise terms, linear perspective can be defined as the procedure for making “a picture on a flat surface in such a manner that the various objects represented in it appear to have the same sizes, shapes, and positions, relatively to each other, that the actual objects as located in actual space would have if seen by the beholder from a single determined point of view.”9 Typically, these images possess a single vanishing point towards which all the parallel lines perpendicular to the picture plane converge, presenting a convincing illusion of depth perception to the viewer.10 Universally acknowledged as a landmark event in the history of art, the advent of linear perspective during the Italian Renaissance has bequeathed us some of the most influential and celebrated paintings in the Western canon. Yet beyond the artistic import of these creations, their geometric constructions participated in a dual process of rationalization of vision and mathematization of space, the ramifications of which extend far and wide.
From the first demonstrations of Filippo Brunelleschi in the early 15th century to the subsequent systematizations of Leon Battista Alberti and Albrecht Dürer, perspectivists developed a set of methods and technical aids for the production of images that simultaneously bear optical verisimilitude to embodied vision and accurately record the relative positions and dimensions of objects within a homogenous space. For James Burke, the impact of the underlying perspective geometry was nothing short of revolutionary:
The new technique permitted the world to be measured through proportional comparison. With the aid of the new geometry the relative sizes of different objects could be assessed at a distance for the first time. Distant objects could be reproduced with fidelity, or created to exact specifications in any position in space and then manipulated mathematically.11
We cannot understate this technique’s central role in the burgeoning scientific worldview. William Ivins notably underlines that “science and technology have advanced in more than direct ratio to the ability of men to contrive methods by which phenomena […] have been brought within the range of visual recognition and measurements and then become subject to that logical symbolization without which rational thought and analysis are impossible.”12
The history of linear perspective and its origins has been the subject of a vast and rich literature, which is neither possible nor useful to fully render here. The appearance of perspective has been variously explained, whether by reference to the advent of a new “worldview” or to practical developments in architecture, workshop practice, surveying, cartography, and astronomy.13 Historians have argued persuasive cases for each of these explanations but no clear consensus exists for the most significant or decisive one. Indeed, the very entanglement of the geometric methods employed across all these domains strongly suggests that there is no single origin to the development of perspective.
Whether it originated or simply cohered alongside the creation of linear perspective, a powerful new worldview certainly came into focus, imbuing a universal and homogenous spatial geometry with profound cultural and intellectual significance. If classical texts of the Ancient World such as Ptolemy’s Geographia (freshly rediscovered in the West in the early 15th century) and Euclid’s Elements of Geometry and Optics no doubt played an important role in the development of linear perspective, it remains nonetheless an original invention of the Italian Renaissance. Classical art’s geometric representations approximated linear perspective but never gave rise to a full and systematic perspectival depiction of space, despite the Ancients having all the required knowledge of geometry. In his landmark essay on Perspective as Symbolic Form, Erwin Panofsky notes the absence of any conception of a homogeneous continuous space in the Ancient World: “they did not do it because that feeling for space which was seeking expression in the plastic arts simply did not demand a systematic space.”14 It is only over the course of the Middle Ages and the Renaissance, Panofsky argues, that modern notions of a homogeneous and isotropic “systematic space” emerge and find artistic expression in linear perspective. The move towards perspectival representation in art in turn supported the emergence of the unified physicalist conception of space that underpinned the new empiricism of the Scientific Revolution and its crowning achievement in Newton’s universal laws of motion. As Richard Tarnas puts it, “it was not peripheral to the emergence of the modern outlook that Renaissance art depicted a world of rationally related solids in a unified space seen from a single objective viewpoint.”15 Most importantly, perspective established a mathematical correspondence between objective physical space and subjective visual space since it assumes the latter is “ordered a priori by an abstract, uniform system of linear coordinates” that faithfully reflects the former.16
Art historians widely credit the Italian architect Filippo Brunelleschi with the first recorded demonstration of linear perspective. Around 1425, Brunelleschi presented a perspectival painting of the Baptistery of St John in Florence for viewing through an intricate set-up. The viewer would stand at the exact location where the work had been painted and peer out from one eye through a small hole at the back of the painting in the direction of the real Baptistery. A mirror would then be raised in front of the viewer, reflecting back the painted image. The created illusion was so compelling that reality and its simulacrum were said to be virtually indistinguishable.17 Although Brunelleschi’s exact method for creating this perspectival image is still debated, his demonstration suggests not merely a certain taste for showmanship but also an astute understanding of optical laws through the precise positioning and size of mirror required for the illusion.18
Martin Kemp argues that Brunelleschi’s architectural background suggests his perspective technique derived from surveying practices.19 In the late Middle Ages, practical geometric techniques of surveying, through such instruments as the cross staff, quadrant, or astrolabe, were increasingly supplemented by the rediscovery of Greek trigonometric theory via the translation and diffusion of Islamic scientific texts. Kim Veltman submits that surveying and perspective are fundamentally entangled since their aims are “essentially the same”: “both seek to record objective elements of the measured world.”20 Perspective and surveying are thus equally exercises in measurement by eye such that “a picture in the modern perspectival style is essentially the outcome of a measuring procedure.”21 Kemp has likewise underlined the strength of the “intersection of geometrical perspective and its related machines with the mathematics of mensuration.”22
The first attempt at formalizing the rules of the linear perspectival representation appears in the 1435 treatise De Pictura by Brunelleschi’s fellow Florentine, Leon Battista Alberti. In common with many of his contemporaries, Alberti granted the eye an exalted status among the senses: “it is such as to be the first, chief, king, like a god of human parts.”23 He explicitly grounded his theory of perspective in optics and Joel Snyder sees in his treatise “the first effort by a painter to establish the certainty of his method of picture construction by deriving it from a scientific account of vision.”24 Although primarily writing for artists, Alberti therefore insisted that “one who is ignorant of geometry will not understand these or any other rules of painting.”25 In practice, the geometric principles employed are again the very same as those found in surveying. Alberti explains that the eye measures distances (or “quantity”) between two points in space with the lines of sight (“visual rays”) to each point “as with a pair of compasses.” In this way, “vision makes a triangle” in which “the base of [this triangle] is the quantity seen and the sides are those rays which are extended from the quantity to the eye.”26 The more acute the angle “within the eye” (i.e. the angle formed by the two lines of sight with each other), the smaller the distance between the two points being observed will appear, a principle familiar to surveyors that captures the universally recognised inverse relationship between distance to an object and visible size. Together, the combined visual rays constitute a “visual pyramid.” Leonardo da Vinci could thus later present perspective as “the demonstrative proof that is confirmed by experience that all things communicate their likenesses to the eye by pyramidal lines; and that the pyramids of bodies of equal magnitudes form a larger or smaller angle according to the kind of distance that there is between one and the other.”27
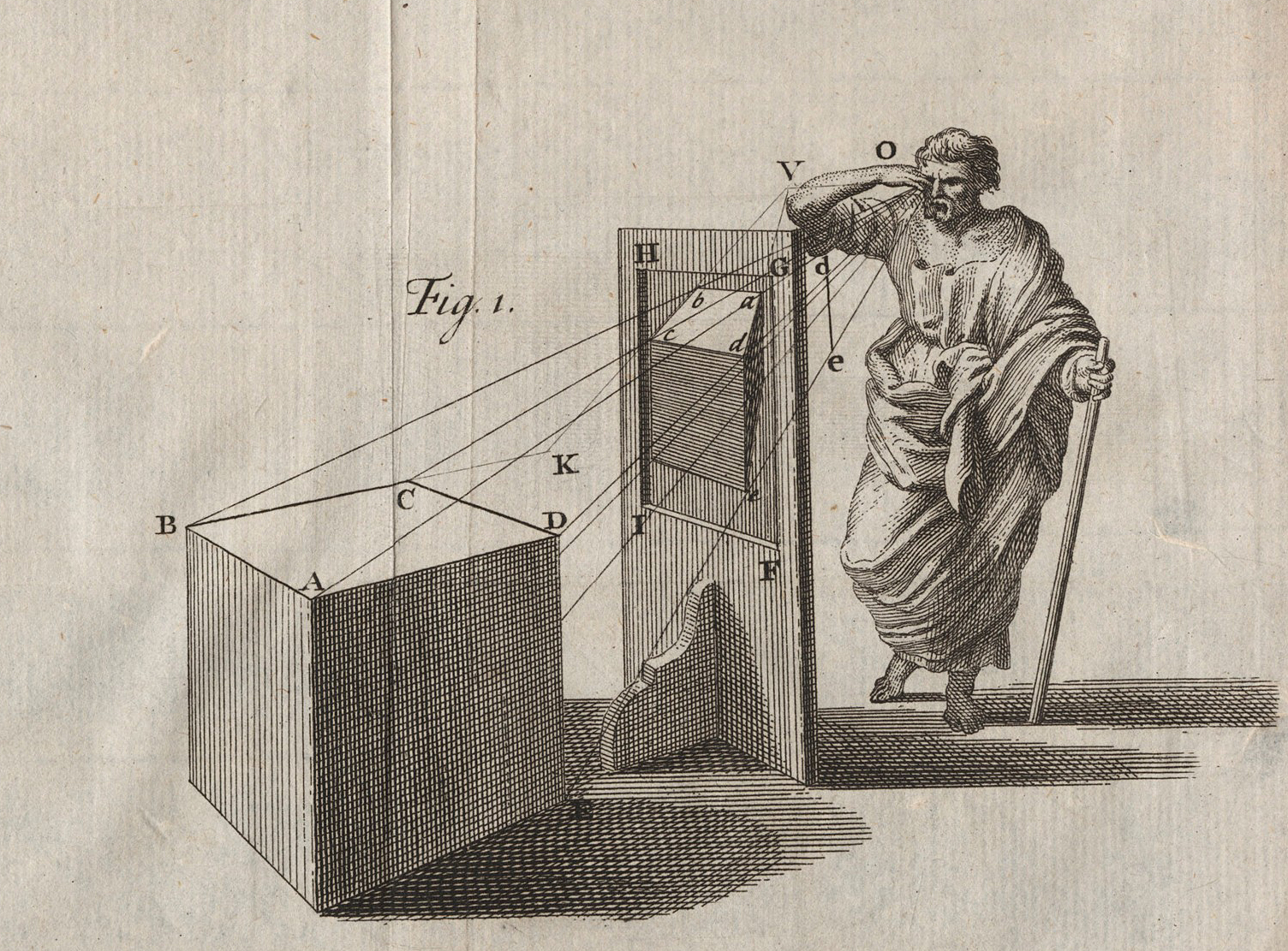
Figure 3: The perspectival image as planar section of the visual pyramid 28
In accordance with this geometric conception of vision, the artist’s picture corresponds to a planar section of the visual pyramid at a given distance. For Alberti, a painting is therefore analogous to “an open window through which I see what I want to paint.”29 Realized in conformity with the established principles of linear perspective, the depicted space appears as an immediate extension of the viewer’s own physical space. Consequently, there can be only one optically correct position from which to view any such representation, at the very apex of the visual pyramid being intersected by the picture plane. In Alberti’s words, “a painted thing can never appear truthful where there is not a definite distance for seeing it.”30 This unique viewpoint is mirrored in the picture by a center point at which the shortest and only perpendicular line of sight – the central ray of the visual pyramid that Alberti dubs “the prince of rays” – arrives on the planar section. In the paradigmatic case of central one-point perspective, the center point coincides with the image’s single vanishing point towards which converge all the lines that are parallel with the viewer’s line of sight (or, put in different but equivalent terms, all the lines perpendicular to the picture plane). Brunelleschi’s elaborate demonstration had indeed already established “the projective coincidence of the point of view and the vanishing point” through the contrivance of the mirror, the single eye of the viewer being required to peer out from the painting’s back panel at the very spot of the vanishing point.31
A perspectival representation thus simultaneously fixes the relative positions and proportions of objects in the depicted space and the location from which that scene is being viewed. The great stillness of Renaissance painting is also that of its viewer. The perspectival image is a two-dimensional plane that opens up simultaneously into the imagined three-dimensional space of the depicted scene and into the real physical space of its singular viewer. For David Martin, the central visual axis of perspective connecting the vanishing point to the viewpoint accordingly presents the viewer with “an image of the self as a visible, objectified, and measurable unit distributed in space.”32 It is worth pausing here to consider the profound implications of the human viewer’s objectivization. Indeed, according to a prominent line of interpretation, linear perspective arranged the visible world “for the spectator as the universe was once thought to be arranged for God”, enthroning the human subject as its new sovereign.33 James Burke asserts that, “at a stroke, the special relationship between God and every separate object was removed, to be replaced by direct human control over objects existing in the same, measurable space.”34 It is indisputable that the nascent humanism of the age was accompanied by an increased capacity for control over a desacralized world. However, the notion that this control issued straightforwardly from a sovereign human subject is problematized when we consider that this very subject was being simultaneously rendered as a new object of rational knowledge located in the same homogenous mathematized space, its embodied perception now subordinated to abstract laws of vision.35 From this point, an inexorable process of disembedding perception from the site of the living organism through the instantiation – initially partial and then increasingly comprehensive – of its mechanisms in technical apparatuses was propelled forward. This deracination should not however be understood as merely the material application of an already established mental abstraction. Rather, the technical marshalling and organisation of perception was intertwined with its theoretical conceptualization from the outset.

Figure 4: The perspectival subject 36
Perspective Machines
Friedrich Kittler observes that in the “artisanal, hand-crafted phase of optical media” characterized by Renaissance painting, its productions would already have been inconceivable “without calculations, and thus they required a technical-scientific foundation.” From this foundation, the “technical apparatus” would develop until it could “detach itself from the eyes and hands of so-called artists and form those absolutely autonomous spheres” that are contemporary “optical media technologies.”37 As William Mitchell puts it, Alberti’s writings ultimately offered nothing less than “a rigorous, step-by-step algorithm for constructing, with drafting instruments, a consistent single-point perspective view of a scene.”38 And it is precisely this “algorithmic character” that has primed perspectival representation for subsequent mechanization and eventual automation.39
Alberti’s geometric instructions to the artist may have been precise and systematic but their application still required a mathematical competence that exceeded most contemporary practitioners. Over the next few centuries, an array of techniques and devices were conceived to assist in the production of perspectivally accurate images. Alberti himself had proposed a grid or velo (veil) which the artist would place between the eye and the represented object, such that it would constitute a plane intersecting the visual pyramid. By fixing the position of their eye, artists could reproduce the details of the model, as seen through the velo, upon a similarly gridded surface. Albrecht Dürer’s influential treatise on perspective, Underweysung der Messung (“instruction of measurement”) presents a similar setup in which a gridded mesh is placed between the artist’s eye and the scene to be represented.40
Dürer also suggests another technique that is of particular interest: a simple instrument that uses a piece of string to mimic the visual rays from the model to the viewer, the respective positions of which can be transferred onto a screen for every point on the model. Without the requirement for any geometric knowledge, the apparatus thus permits the methodical projection of individual points in three-dimensional space onto a two-dimensional picture plane. Dürer’s device is noteworthy for making explicit the act of measurement involved in the perspectival system of pictorial representation.41 Perhaps most significantly, however, it “eliminates the human eye altogether”,42 thus marking an early instantiation of the efforts aimed at “the mechanization of the perspective painting and of the arrested eye” that would eventually culminate in the invention of photography.43
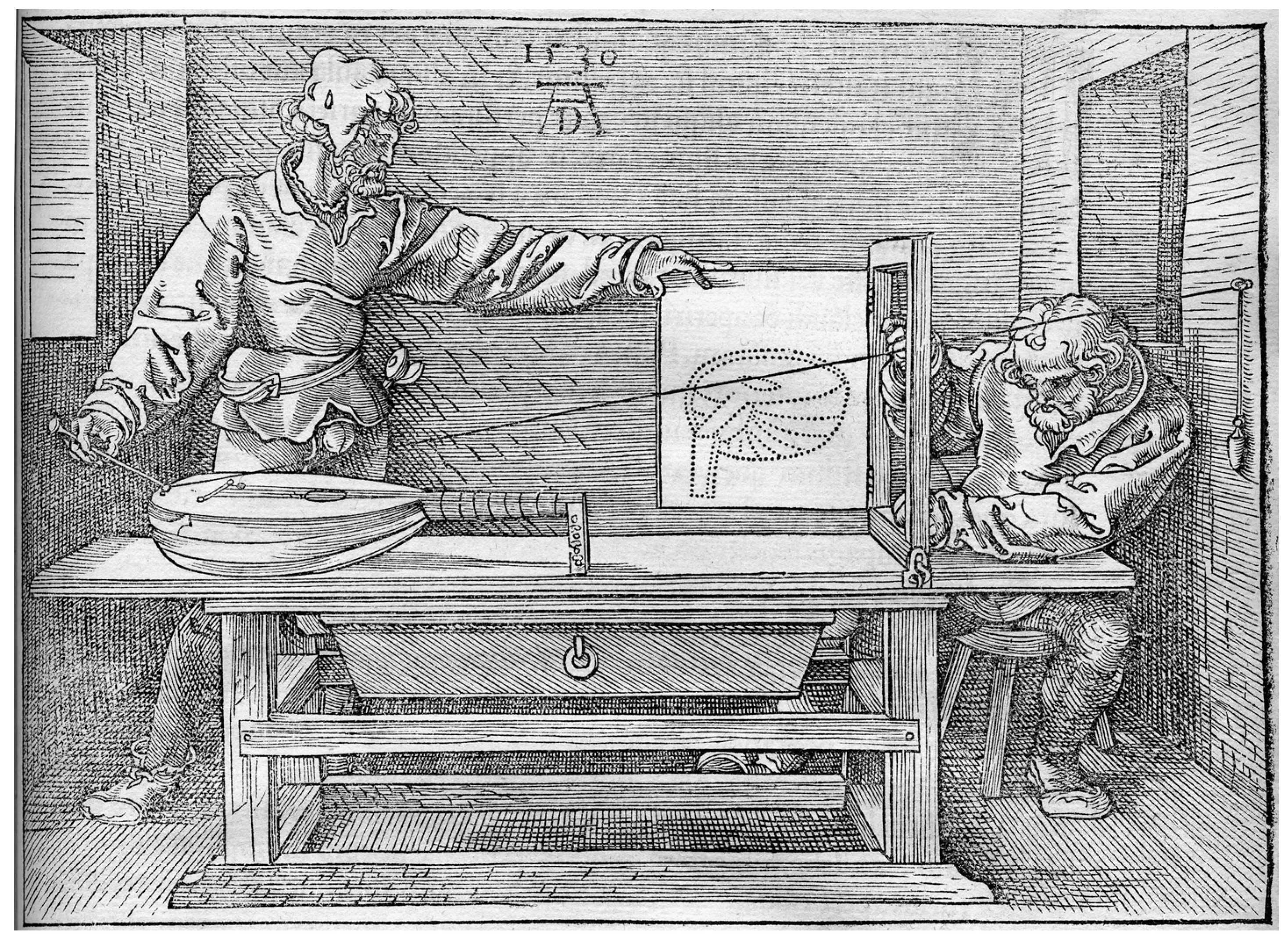
Figure 5: Draughtsmen with lute 44
Such instruments’ further development and diffusion were crucial in making perspective accessible to practitioners unschooled in the finer points of geometry and in widening its range of applications, notably in the military field. Thus the introduction to the 1583 edition of Vignola’s treatise on “practical perspective” submits that:
the practice of this most delightful art [i.e. of perspective], which besides the many useful things it brings to the military arts, is also particularly important in the construction and defence of forts, since one can with the instruments of these arts draw in outline whatever site one wants without trouble and one will have not only the plane but also the elevation in its every detail and the measure of its parts will be proportionate to the distance which there is between our eye and the things we have measured in our drawing.45
Over the next two centuries, numerous works were produced to educate military staff into the practical applications of perspective and geometric drawing, from the design of fortifications to the production of maps to the deployment of troops on the battlefield. As Veltman notes, these manuals typically bypassed the underlying geometric theory since a range of instruments could produce perspectival representations without the requirement of specialist knowledge by the user.46 Such instruments included variants of grid or string methods and adaptations of the Jacob’s staff, quadrant, or astrolabe.
While not devoid of aesthetic appeal, the perspectival representations thereby produced were eminently practical. They provided accurate information about the relative proportions and positions of objects in space, which was plainly valuable to the planning and conduct of military operations. Pietro Accolti’s 1625 work Lo Inganno de gl’occhi (“the deception of the eyes”) details how, from the perspectival drawing of a fortress, “it is possible to reconstruct the layout of the building by applying the perspective procedure inversely” through the means of Dürer’s string technique.47 Reconnaissance missions could, from a safe distance and through the assistance of appropriate instruments, produce a perspectival representation of a given site from which an accurate survey map could be subsequently composed. Such a map could then assist in the conduct of any future siege, an activity central to the practice of warfare in Europe until the late 18th century.
The above techniques underscore that a practical understanding of different forms of geometric projection and the conservation of spatial proportions in converting them developed alongside the invention of linear perspective. Joan Gadol notably argues that Alberti’s extensive work on surveying and cartography indicates that he already recognized a “strict, technical connection” between the perspectival picture and the map through their common reliance on a projective geometry designed to preserve the relative distances and dimensions of objects in their translation onto a two-dimensional plane.48 However, the comprehensive formalization of the common projective geometry that underlay these practical methods would only be realized through an incremental intellectual endeavour that would not be fully completed until the 19th century.
A Generalized Projective Geometry
The history of linear perspective intersects with the development of another form of graphical projection, one that was commonly employed for plans of fortifications or war machines because of its especially convenient representation of spatial measurements. So-called “military” or “soldier’s” perspective is a form of geometric projection with no vanishing point and where all the parallel lines of the depicted object remain parallel in the image. The value of such a parallel or “orthographic” projection is that it avoids the visual distortion of classical perspective known as foreshortening. Instead, the projection maintains the measured dimensions of all the forms represented at a single constant scale. Such a property is of particular utility to architects and engineers, notably for the representation of fortifications or war machines. The use of this graphic form, albeit frequently lacking in geometrical rigor, preceded the Renaissance discovery of linear perspective and continued to develop primarily within the distinct literature of technical drawing.49 Yet the linear and military perspectives would eventually be conjoined when it was grasped they could both be treated as merely variants of a wider projective geometry. Indeed, military perspective can be defined as a zero-point perspective that produces an image in which the viewpoint is set at an infinite distance, effectively a “view from nowhere.”
Figure 6: Military architecture presented in “soldier’s perspective” 50
The establishment of a general projective geometry is commonly attributed to the 17th century architect and mathematician Girard Desargues. Through his efforts for devising a new method for the construction of perspectival images, Desargues formulated the crucial notion of the “point at infinity.” Desargues postulated that all parallel lines within a projective plane meet at a point at infinity, just as they do at the vanishing point of a central perspective image but with this property now expressed as the founding axiom of a generalized mathematics of projection.51 If his breakthrough was not fully appreciated until Gaspard Monge’s and Jean-Victor Poncelet’s investigations in the early 19th century, Desargues nevertheless marks the moment when, in the words of Erwin Panofsky, “perspective, replacing for the first time the single Euclidean ‘visual cone’ with the universal ‘geometrical beam,’ abstracted itself completely from the line of sight and thus opened up all spatial directions equally.”52 Indeed, projective geometry seeks to formally establish the properties of a represented object that remain invariant as the viewer moves from one visual perspective to another – to determine the spatial relations that remain constant regardless of the position of the “eye.” Projective geometry therefore provides a theoretical understanding of the properties of a Euclidean space that can be extracted from any of its perspectival representations, along with furnishing all the mathematical tools necessary for doing so. By the same token, the position in space of the singular viewpoint for any given perspectival image can be determined rigorously, as with the formal technique proposed in 1759 by the mathematician Johann Heinrich Lambert in his pursuit of the “inverse rules of perspective.”53
Although already implicit in the first linear perspective images, the formulation of a general projective geometry effectively completed the rationalization of vision initiated in the Renaissance. It definitively established a rigorous mathematical correspondence between absolute physical space and any of its possible perspectival representations. The rules of projective geometry would provide a standard by which the spatial fidelity of visual perception could be gauged, simultaneously displacing and devaluing innate phenomenological experience. In this spirit, the 17th century artist Abraham Bosse, a student under Desargues and a lifelong promoter of his ideas, would affirm that painting’s true task was not to represent things “as the eye sees them or believes it sees them, but such as the laws of perspective impose them on our reason.”54
In the present day, the branch of projective geometry that has incorporated linear perspective underlies the techniques employed in fields as varied as photogrammetry, cartography, computer vision, and 3D graphics. Perspectival geometry thus supports the deployment of an array of apparatuses for the visual recording, measurement, and representation of the relative positions and proportions of objects in space. This is not to say that perspective still occupies the sole or even primary role in the contemporary socio-technical organization of perception. In many instances, it has given way to other perceptual techniques that do not rest upon classical optics and extend across the electromagnetic spectrum of light, such as radar, infrared, or laser. Linear perspective has however been critical in founding what Lev Manovich refers to as “visual nominalism”, understood as “the use of vision to capture the identity of individual objects and spaces by recording distances and shapes” and “create detailed maps of three-dimensional reality.”55 If a perceptual nominalism now extends far beyond the narrow confines of visible light and accordingly relies on different sets of scientific principles, it remains nonetheless fundamentally tributary to that originary geometric correlation of vision and space. Last but not least, the discovery of linear perspective set in motion an autonomization of perception and spatial reasoning whose technical realization is today still unfolding before our own humbled eyes.





